
题目列表(包括答案和解析)
(本小题满分12分)
四个大小相同的小球分别标有数字1、1、2、2,把它们放在一个盒子里,从中任意摸出两个小球,它们所标有的数字分别为 、
、 ,记
,记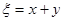 ;
;
(Ⅰ)求随机变量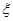 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设“函数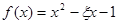 在区间
在区间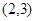 上有且只有一个零点”为事件
上有且只有一个零点”为事件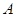 ,求事件
,求事件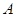 发生的概率.
发生的概率.
(本小题满分12分)
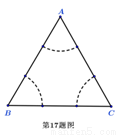
某射击运动员进行射击训练,前三次射击在靶上的着弹点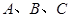 刚好是边长为
刚好是边长为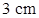 的等边三角形的三个顶点.
的等边三角形的三个顶点.
(Ⅰ)第四次射击时,该运动员瞄准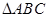 区域射击(不会打到
区域射击(不会打到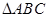 外),则此次射击的着弹点距
外),则此次射击的着弹点距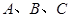 的距离都超过
的距离都超过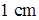 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ)
该运动员前三次射击的成绩(环数)都在区间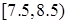 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间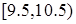 内.现从这
内.现从这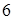 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为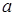 和
和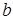 )进行技术分析.求事件“
)进行技术分析.求事件“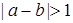 ”的概率.
”的概率.
(本小题满分12分)
四个大小相同的小球分别标有数字1、1、2、2,把它们放在一个盒子中,从中任意摸
出两个小球,它们的标号分别为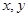 ,记
,记 .
.
(1)求随机变量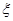 的分布列及数学期望;
的分布列及数学期望;
(2)设“函数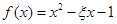 在区间(2,3)上有且只有一个零点”为事件
在区间(2,3)上有且只有一个零点”为事件 ,求事件
,求事件
 发生的概率.
发生的概率.
(本小题满分12分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
|
环数 |
7 |
8 |
9 |
10 |
|
命中次数 |
2 |
7 |
8 |
3 |
(1)求此运动员射击的环数的平均值;
(2)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为 次、
次、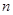 次,每个基本事件为
次,每个基本事件为 ,求事件
,求事件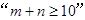 的概率。
的概率。
(本小题满分12分)![]() 个正数排成一个
个正数排成一个![]() 行
行![]() 列的数阵:
列的数阵:
| 第1列 | 第2列 | 第3列 | … | 第 | |
| 第1行 |
|
|
| … |
|
| 第2行 |
|
|
| … |
|
| 第3行 |
|
|
| … |
|
| … | … | … | … | … | … |
| 第 |
|
|
| … |
|
其中![]() 表示该数阵中位于第
表示该数阵中位于第![]() 行第
行第![]() 列的数。已知该数阵每一行的数成等差数列,每一列的数成公比为2的等比数列,
列的数。已知该数阵每一行的数成等差数列,每一列的数成公比为2的等比数列,![]()
(1)求![]() ; (2)设
; (2)设![]() ,求
,求![]() ;
;
(3)在(2)的条件下,若不等式![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的最大值。
的最大值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com