
题目列表(包括答案和解析)
求实数![]() 的取值范围,使关于
的取值范围,使关于![]() 的方程
的方程![]()
⑴有两个实根,且一个比2大,一个比2小;
⑵有两个实数根,且都比1大;
⑶有两实数根![]() ,
,![]() ,且满足
,且满足![]() ;
;
⑷至少有一个正根.
 的取值范围,使关于
的取值范围,使关于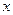 的方程
的方程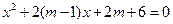
 ,
, ,且满足
,且满足 ;
;已知函数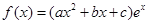 在
在 上单调递减,且满足
上单调递减,且满足 ,
,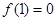 (Ⅰ) 求
(Ⅰ) 求 的取值范围;(Ⅱ)设
的取值范围;(Ⅱ)设 ,求在
,求在 上的最大值和最小值
上的最大值和最小值
已知函数 .
.
(1)若 ,当
,当 时,求
时,求 的取值范围;
的取值范围;
(2)若定义在 上奇函数
上奇函数 满足
满足 ,且当
,且当 时,
时, ,求
,求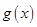 在
在 上的反函数
上的反函数 ;
;
(3)若关于 的不等式
的不等式 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)若 ,当
,当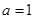 时,求
时,求 的取值范围;
的取值范围;
(2)若定义在 上奇函数
上奇函数 满足
满足 ,且当
,且当 时,
时, ,求
,求 在
在 上的反函数
上的反函数 ;
;
(3)对于(2)中的 ,若关于
,若关于 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
1、A 2、B 3、B 4、D 5、C 6、C
 7、
7、 8、
8、 9、0
10、
9、0
10、
11、【解】(1)
∴NP为AM的垂直平分线,∴|NA|=|NM|.…………………………2分
又
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.
且椭圆长轴长为 焦距
焦距 ……………5分
……………5分
∴曲线E的方程为 ………………6分
………………6分
(2)当直线GH斜率存在时,
设直线GH方程为
得
设 ……………………8分
……………………8分

 ,
,
 ……………………10分
……………………10分


又当直线GH斜率不存在,方程为
 ……………………………………12分
……………………………………12分
12、【解】(1)由题设知
由于 ,则有
,则有 ,所以点A的坐标为
,所以点A的坐标为 ,
,
故 所在直线方程为
所在直线方程为 ,
………………………………3分
,
………………………………3分
所以坐标原点O到直线 的距离为
的距离为 ,
,
又 ,所以
,所以 ,解得
,解得 ,
,
所求椭圆的方程为 .……………………………………………5分
.……………………………………………5分
(2)由题意知直线l的斜率存在,设直线l的方程为 ,则有
,则有 ,
,
设 ,由于
,由于 ,
,
∴ ,解得
,解得 …………………8分
…………………8分
又Q在椭圆C上,得 ,
,
解得 ,
…………………………………………………………………………10分
,
…………………………………………………………………………10分
故直线l的方程为 或
或 ,
,
即 或
或 . ……………………………………………12分
. ……………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com