练习册

  • 练习册
  • 试题
    A． B． C． D． 3.如右图.一个简单空间几何体的三视图其主视图与左视图 【查看更多】

     

    题目列表(包括答案和解析)

    如右图，A、B、C、D是某煤矿的四个采煤点，l是公路，图中所标线段为道路，ABQP、BCRQ、CDSR近似于正方形．已知A、B、C、D四个采煤点每天的采煤量之比约为5∶1∶2∶3，运煤的费用与运煤的路程、所运煤的重量都成正比．现要从P、Q、R、S中选出一处设立一个运煤中转站，使四个采煤点的煤运到中转站的费用最少，则地点应选在

    [　　]

    A．P点　　　　B．R点　　　　C．Q点　　　　D．S点

    查看答案和解析>>

    如图，椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的左、右焦点分别为F1，F2，上顶点为A，在x轴负半轴上有一点B，满足AB⊥AF2．且F1为BF2的中点．
    （1）求椭圆C的离心率；
    （2）D是过A，B，F2三点的圆上的点，D到直线l：x-
    		3
    y-3=0的最大距离等于椭圆长轴的长，求椭圆C的方程．

    查看答案和解析>>

    在右图中，实线所围成的多边形区域是由四个全等正方形边接边所形成的．现若补上图中标有号码的其中一个全等正方形，如此则可得九个多边形区域（每个区域恰含有五个全等正方形），则这九个多边形区域中，可折叠成一无盖的正立方体容器的有（　　）

    查看答案和解析>>

    如图，已知椭圆＝1(a＞b＞0)的离心率为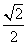，以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(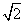＋1)，一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上异于顶点的任一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D.

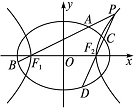
    (1)求椭圆和双曲线的标准方程；

    (2)设直线PF1、PF2的斜率分别为k1、k2，证明：k1·k2＝1；

    (3)是否存在常数λ，使得|AB|＋|CD|＝λ|AB|·|CD|恒成立？若存在，求λ的值；若不存在，请说明理由．

     

    查看答案和解析>>

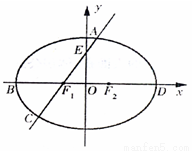
    如图，在椭圆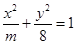中，F1，F2分别为椭圆的左、右焦点，B、D分别

    为椭圆的左、右顶点，A为椭圆在第一象限内的一点，直线AF1交椭圆于另

    一点C，交y轴于点E，且点F1、F2三等分线段BD．

    （1）求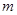的值；

    （2）若四边形EBCF2为平行四边形，求点C的坐标；

    （3）当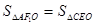时，求直线AC的方程．

     

     

    查看答案和解析>>

    1、D    2、C   3、C    4、C    5、B    6、C

    7、4    8、   9、   10、   

    11、解：（Ⅰ）∵   底面ABCD是正方形，

    ∴AB⊥BC,

    又平面PBC⊥底面ABCD  

    平面PBC ∩  平面ABCD=BC

    ∴AB  ⊥平面PBC

    又PC平面PBC

    ∴AB  ⊥CP  ………………3分

    （Ⅱ）解法一：体积法.由题意，面面，

     

    取中点，则

    面.

    再取中点，则   ………………5分

    设点到平面的距离为，则由

    .                   ………………7分

    解法二：面

    取中点，再取中点

    ，

    过点作，则

    在中，

    由

    ∴点到平面的距离为。  ………………7分

    （Ⅲ）

    面

    就是二面角的平面角.

    ∴二面角的大小为45°.   ………………12分

     

    12、解：（I）证明：在直棱柱ABC-A1B1C1中，有A1C1⊥CC1。

         ∵ ∠ACB＝90º，∴A1C1⊥C1B1，即A1C1⊥平面C1CBB1，

       ∵CG平面C1CBB1,∴A1C1⊥CG。┉┉┉┉┉┉┉┉2分

       在矩形C1CBB1中，CC1＝BB1＝2BC，G为BB1的中点，

       CG＝BC，C1G＝BC，CC1＝2BC

       ∴∠CGC1＝90，即CG⊥C1G┉┉┉┉┉┉┉┉4分

    而A1C1∩C1G=C1，

    ∴CG⊥平面A1GC1。

    ∴平面A1CG⊥平面A1GC1。┉┉┉┉┉┉┉┉6分

    （II）由于CC1平面ABC，

     ∠ACB＝90º，建立如图所示的空间坐标系，设AC＝BC＝CC1＝a，则A(a,0,0),B(0,a,0)

    A1(a,0,2a),G(0,a,a).

    ∴=(a,0,2a),=(0,a,a). ┉┉┉┉┉┉┉┉8分

    设平面A1CG的法向量n1=(x1,y1,z1),

    由得

    令z1=1,n1=(-2,-1,1). ┉┉┉┉┉┉┉┉9分

    又平面ABC的法向量为n2=(0,0,1) ┉┉┉┉┉┉┉┉10分

    设平面ABC与平面A1CG所成锐二面角的平面角为θ，

    则┉┉┉┉┉┉┉┉11分

    即平面ABC与平面A1CG所成锐二面角的平面角的余弦值为。┉┉┉12分

     

     

     

     


    同步练习册答案