(本小题满分13分)

甲、乙两台机床生产同一型号零件．记生产的零件的尺寸为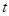(cm)，相关行业质检部门规定：若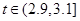，则该零件为优等品；若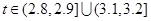，则该零件为中等品；其余零件为次品．现分别从甲、乙机床生产的零件中各随机抽取50件，经质量检测得到下表数据：

（Ⅰ）设生产每件产品的利润为：优等品3元，中等品1元，次品亏本1元. 若将频率视为概率，试根据样本估计总体的思想，估算甲机床生产一件零件的利润的数学期望；

（Ⅱ）对于这两台机床生产的零件，在排除其它因素影响的情况下，试根据样本估计总体的思想，估计约有多大的把握认为“零件优等与否和所用机床有关”，并说明理由.

参考公式：.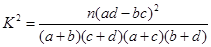

参考数据：

  (本小题满分12分)

甲、乙两台机床在相同的技术条件下，同时生产一种零件，现在从中抽测10个，它们的尺寸分别如下（单位：mm）.

甲机床：10.2  10.1  10   9.8   9.9  10.3   9.7   10   9.9   10.1；

乙机床：10.3  10.4  9.6  9.9  10.1  10.9   8.9   9.7  10.2  10.

分别计算上面两个样本的平均数和方差.如图纸规定零件的尺寸为10 mm，从计算的结果来看哪台机床加工这种零件较合适？

  (本小题满分12分)

甲、乙两台机床在相同的技术条件下，同时生产一种零件，现在从中抽测10个，它们的尺寸分别如下（单位：mm）.

甲机床：10.2  10.1  10   9.8   9.9  10.3   9.7   10   9.9   10.1；

乙机床：10.3  10.4  9.6  9.9  10.1  10.9   8.9   9.7  10.2  10.

分别计算上面两个样本的平均数和方差.如图纸规定零件的尺寸为10 mm，从计算的结果来看哪台机床加工这种零件较合适？

(本小题满分13分)甲、乙、丙三人参加了一家公司招聘面试，甲表示只要面试合格就签约；乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约，设每人面试合格的概率都是，且面试是否合格互不影响。（1）求至少有一人面试合格的概率；（2）求签约人数的分布列和数学期望；

(本小题满分13分)

甲、乙二人用4张扑克牌（分别是红桃2、红桃3、红桃4、方块4）玩游戏，他们将扑克牌洗匀后，背面朝上放在桌面上，甲先抽，乙后抽，抽出的牌不放回，各抽一张。

（1）设分别表示甲、乙抽到的牌的数字，写出甲、乙二人抽到的牌的所有情况

（2）若甲抽到红桃3，则乙抽到的牌面数字比3大的概率是多少？

（3）甲、乙约定：若甲抽到的牌的牌面数字比乙大，则甲胜；否则，乙胜。你认为此游戏是否公平？请说明你的理由.