
题目列表(包括答案和解析)
(本小题14分)某人有楼房一幢,室内面积共计180m2,拟分割成两类房间作为旅游客房,大房间每间面积为18m2,可住游客5名,每名游客每天住宿费40元;小房间每间面积为15m2,可以住游客3名,每名游客每天住宿费50元;装修大房间每间需要1000元,装修小房间每间需要600元.如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,每天能获得最大的房租收益?(注:设分割大房间为x间,小房间为y间,每天的房租收益为z元)
(1)写出x,y所满足的线性约束条件;
(2)写出目标函数的表达式;
(3)求x,y各为多少时,每天能获得最大的房租收益?每天能获得最大的房租收益是多少?
(本小题14分)已知 中,
中, 的对边分别为
的对边分别为 ,且
,且 ,
,  .(1)若
.(1)若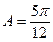 ,求边
,求边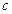 的大小; (2)求
的大小; (2)求 边上高的最大值.
边上高的最大值.
(本小题14分)已知函数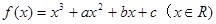 在
在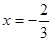 处取得极值,其图象在点
处取得极值,其图象在点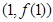 处的切线与直线
处的切线与直线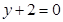 平行(1)求
平行(1)求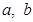 的值;
的值;
(2)若对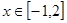 都有
都有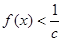 恒成立,求
恒成立,求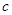 的取值范围。
的取值范围。
(本小题14分)已知![]() 中,
中,![]() 的对边分别为
的对边分别为![]() ,且
,且![]() ,
, ![]() .(1)若
.(1)若![]() ,求边
,求边![]() 的大小; (2)求
的大小; (2)求![]() 边上高的最大值.
边上高的最大值.
(本小题14分)如图,在平面直角坐标系xoy中,设点F(0, p)(p>0), 直线l : y= -p, 点P在直线l上移动,R是线段PF与x轴的交点, 过R、P分别作直线 、
、 ,使
,使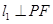 ,
,
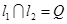 .
.
(1) 求动点 的轨迹
的轨迹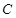 的方程;
的方程;
(2)在直线 上任取一点
上任取一点 做曲线
做曲线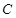 的两条切线,设切点为
的两条切线,设切点为 、
、 ,求证:直线
,求证:直线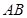 恒过一定点.
恒过一定点.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com