
题目列表(包括答案和解析)
对于函数![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,称
成立,称![]() 为不动点,已知函数
为不动点,已知函数![]()
当![]() 时,求函数
时,求函数![]() 不动点.
不动点.
(2)若对任意的实数![]() ,函数
,函数![]() 恒有两个相异的不动点,求a的取值范围.
恒有两个相异的不动点,求a的取值范围.
 .
. 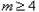 时,求
时,求 的单调递增区间;
的单调递增区间; ,使得对任意的
,使得对任意的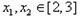 ,都有
,都有 恒成立.若存在,求出
恒成立.若存在,求出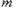 的取值范围; 若不存在,请说明理由。
的取值范围; 若不存在,请说明理由。(14分)设函数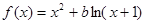 ,其中
,其中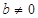 .
.
(Ⅰ)若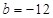 ,求
,求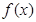 在
在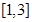 上的最小值;
上的最小值;
(Ⅱ)如果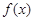 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数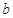 的取值范围;
的取值范围;
(Ⅲ)是否存在最小的正整数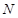 ,使得当
,使得当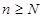 时,不等式
时,不等式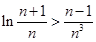 恒成立.
恒成立.
设函数 ,其中
,其中 .(Ⅰ)若
.(Ⅰ)若 ,求
,求 在
在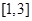 上的最小值;
上的最小值;
(Ⅱ)如果 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围;
(Ⅲ)是否存在最小的正整数 ,使得当
,使得当 时,不等式
时,不等式 恒成立.
恒成立.
设函数 ,其中
,其中 .(Ⅰ)若
.(Ⅰ)若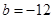 ,求
,求 在
在 上的最小值;
上的最小值;
(Ⅱ)如果 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围;
(Ⅲ)是否存在最小的正整数 ,使得当
,使得当 时,不等式
时,不等式 恒成立.
恒成立.
一:选择题:BCAAD CCCBA CC
二:填空题:
|