
题目列表(包括答案和解析)
(本小题满分12分)设 是实数,对函数
是实数,对函数 和抛物线
和抛物线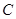 :
: ,有如下两个命题:
,有如下两个命题: 函数
函数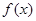 的最小值小于0;
的最小值小于0; 抛物线
抛物线 上的点
上的点 到其准线的距离
到其准线的距离 .
.
已知“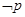 ”和“
”和“
 ”都为假命题,求
”都为假命题,求 的取值范围.
的取值范围.
(本小题满分12分)设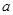 是实数,对函数
是实数,对函数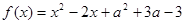 和抛物线
和抛物线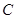 :
: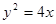 ,有如下两个命题:
,有如下两个命题: 函数
函数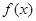 的最小值小于0;
的最小值小于0;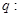 抛物线
抛物线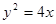 上的点
上的点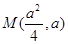 到其准线的距离
到其准线的距离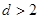 .
.
已知“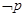 ”和“
”和“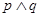
 ”都为假命题,求
”都为假命题,求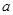 的取值范围.
的取值范围.
 是实数,对函数
是实数,对函数 和抛物线
和抛物线 :
: ,有如下两个命题:
,有如下两个命题: 函数
函数 的最小值小于0;
的最小值小于0; 抛物线
抛物线 上的点
上的点 到其准线的距离
到其准线的距离 .
. ”和“
”和“
 ”都为假命题,求
”都为假命题,求 的取值范围.
的取值范围. (本小题满分12分)已知函数f(x)=x3+x2-2.
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点(an,an+12-2an+1)(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值.
(本小题满分12分) 已知函数 .
.
(1) 设F(x)=
 在
在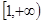 上单调递增,求
上单调递增,求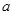 的取值范围。
的取值范围。
(2)若函数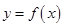 与
与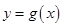 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求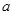 的取值范围;
的取值范围;
(3)在(2)的条件下,过线段MN的中点作 轴的垂线分别与
轴的垂线分别与 的图像和
的图像和 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作 的切线
的切线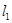 ,以T为切点作
,以T为切点作 的切线
的切线 .是否存在实数
.是否存在实数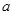 使得
使得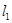
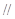
 ,如果存在,求出
,如果存在,求出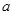 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com