
题目列表(包括答案和解析)
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)某市公租房的房源位于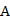 、
、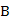 、
、 三个片区.设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的.求该市的4位申请人中:
三个片区.设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的.求该市的4位申请人中:
(Ⅰ)没有人申请A片区房源的概率;
(Ⅱ)每个片区的房源都有人申请的概率.
(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)设函数 =
=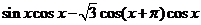 (
(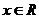 ).
).
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)若函数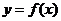 的图象按
的图象按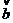 =(
=(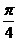 ,
,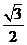 )平移后得到函数
)平移后得到函数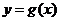 的图象,求
的图象,求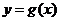 在[0,
在[0,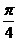 ]上的最大值.
]上的最大值.
(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)设{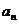 }是公比为正数的等比数列,
}是公比为正数的等比数列, =2,
=2,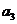 =
=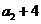 .
.
(Ⅰ)求{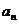 }的通项公式;
}的通项公式;
(Ⅱ)设{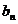 }是首项为1,公差为2的等差数列,求数列{
}是首项为1,公差为2的等差数列,求数列{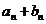 }的前
}的前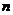 项和
项和 .
.
(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)
设函数![]() .
.
(Ⅰ)求![]() 的最小正周期.
的最小正周期. ![]()
![]()
(Ⅱ)若函数![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称,求当
对称,求当![]() 时
时![]() 的最大值.
的最大值.
(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为![]() 和
和![]() ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数![]() 的分布列与期望.
的分布列与期望. ![]()
![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com