
题目列表(包括答案和解析)
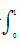 (
( -x)dx的值为( )。
-x)dx的值为( )。为了保护一种珍贵文物,博物馆需要在一种无色玻璃的密封保护罩内充入保护气体。假设博物馆需要支付的总费用由两部分组成:①罩内该种气体的体积比保护罩的容积少0.5立方米,且每立方米气体费用为1千元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为8千元。
(1)求博物馆支付总费用y与保护罩容积V之间的函数关系式;
(2)求博物馆支付总费用的最小值。
P, Q分别为∠A0B两边上的两个动点,若![]() ,△POQ的面积为定值8,求
,△POQ的面积为定值8,求
(1)P, Q中点M的轨迹方程;
(2)![]() 的最小值。
的最小值。
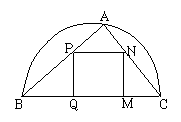 (满分14分)如图,某园林单位准备绿化一块直径为BC的半圆形空间,△ABC外的地方种草,△ABC的内接正方形MNPQ为水池,其余地方种花。若BC=a,∠ABC=
(满分14分)如图,某园林单位准备绿化一块直径为BC的半圆形空间,△ABC外的地方种草,△ABC的内接正方形MNPQ为水池,其余地方种花。若BC=a,∠ABC= ,设△ABC面积为S1,正方形MNPQ的面积为S2.
,设△ABC面积为S1,正方形MNPQ的面积为S2.
(1)用a, 表示S1,S2;
表示S1,S2;
(2)当a固定, 变化时,求
变化时,求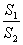 最小值及此时
最小值及此时 值.
值.
 (本题满分14分)
(本题满分14分)
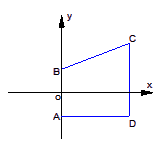
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(1)求动点C的轨迹E的方程;
(2)试探究在轨迹E上是否存在一点P?使得P到直线y=x-2的
距离最短;
(3)设轨迹E与直线![]() 所围成的图形的
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com