
题目列表(包括答案和解析)
.(本小题满分12分)
如图,在四梭锥中S-ABCD中,AB上AD,AB∥CD,CD=3AB=3,平面SAD上平面ABCD,E是线段AD上一点,AE=ED=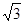 ,SE⊥AD.
,SE⊥AD.
(I)证明:平面SBE⊥平面SEC,
(Ⅱ)若SE=1.求三棱锥E-SBC的高。
(本小题满分12分)
设n为正整数,规定:fn(x)=![]() ,已知f(x)= .
,已知f(x)= .
(1)解不等式f(x)≤x;
(2)设集合A={0,1,2},对任意x∈A,证明f3(x)=x;
(3)求f2007()的值;
(4)(理)若集合B=,证明B中至少包含8个元素.
(本小题满分12分)
设n为正整数,规定:fn(x)=![]() ,已知f(x)= .
,已知f(x)= .
(1)解不等式f(x)≤x;
(2)设集合A={0,1,2},对任意x∈A,证明f3(x)=x;
(3)求f2007()的值;
(4)(理)若集合B=,证明B中至少包含8个元素.
.(本小题满分12分)
设函数f(x)=lnx-p(x-1),p∈R.
(Ⅰ)当p=1时,求函数f(x)的单调区间;
(Ⅱ)设函数g(x)=xf(x)+p(2x2―x―1),(x≥1),求证:当p≤-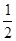 时,有g(x)≤0成立.
时,有g(x)≤0成立.
(本小题满分12分)
已知数列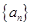 中,
中,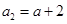 (
( 为常数),
为常数),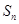 为
为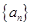 的前
的前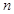 项和,且
项和,且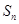 是
是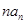 与
与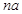 的等差中项.
的等差中项.
(Ⅰ)求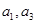 并归纳出
并归纳出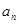 (不用证明);[来源:学+科+网]
(不用证明);[来源:学+科+网]
(Ⅱ)若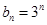 且
且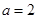 ,求数列
,求数列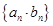 的前
的前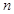 项和
项和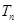 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com