(本小题满分13分)

某化工企业生产某种产品，生产每件产品的成本为3元，根据市场调查，预计每件产品的出厂价为x元(7≤x≤10)时，一年的产量为(11 – x)²万件；若该企业所生产的产品能全部销售，则称该企业正常生产；但为了保护环境，用于污染治理的费用与产量成正比，比例系数为常数a (1≤a≤3)．

（Ⅰ）求该企业正常生产一年的利润L (x)与出厂价x的函数关系式；        

（Ⅱ）当每件产品的出厂价定为多少元时，企业一年的利润最大，并求最大利润．

 (本小题满分13分)

某市物价局调查了某种治疗H1N1流感的常规药品在2009年每个月的批发价格和该药品在药店的销售价格，调查发现，该药品的批发价格按月份以12元/盒为中心价随某一正弦曲线上下波动，且3月份的批发价格最高为14元/盒，7月份的批发价格最低为10元/盒.该药品在药店的销售价格按月份以14元/盒为中心价随另一正弦曲线上下波动，且5月份的销售价格最高为16元/盒，9月份的销售价格最低为12元/盒.

（Ⅰ）求该药品每盒的批发价格f(x)和销售价格g(x)关于月份的函数解析式；

（Ⅱ）假设某药店每月初都购进这种药品p 盒，且当月售完，求该药店在2009年哪些月份是盈利的？说明你的理由.

（本小题满分13分）

某商场销售某种商品的经验表明，该商品每日的销售量y（单位：千克）与销售价格x（单位：元/千克）满足关系式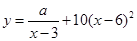，其中3<x<6，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克。

（I）求a的值

（II）若该商品的成品为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大。

（本小题满分13分）

某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元。该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不低于51元

（1）当一次订购量为多少个时，零件的实际出厂单价恰降为51元？

（2）设一次订购量为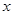个，零件的实际出厂单价为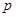元，写出函数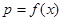的表达式；

（3）当销售商一次订购多少个时，该厂获得的利润为6000元？（工厂售出一个零件的利润=实际出厂单价—成本）

（本小题满分13分）

某商场销售某种商品的经验表明，该商品每日的销售量y（单位：千克）与销售价格x（单位：元/千克）满足关系式，其中3<x<6，a为常数，已知销售价格为5元/千克时，每日可售出该商品11千克。

（I）求a的值

（II）若该商品的成品为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大。