
题目列表(包括答案和解析)
| 男 | 女 | 总计 | |
| 走天桥 | 40 | 20 | 60 |
| 走斑马线 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.05 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 110×(40×30-20×20) |
| 60×50×60×50 |
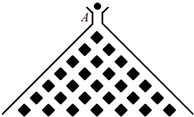 (2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
(2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是| 1 |
| 2 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com