
题目列表(包括答案和解析)
(本题满分15分) 设函数![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时,![]() ,且对于任意的实数
,且对于任意的实数![]() 、
、![]() ,都有
,都有![]() .(1)求
.(1)求![]() ;(2)试判断函数
;(2)试判断函数![]() 在
在![]() 上是否存在最小值,若存在,求该最小值;若不存在,说明理由;(3)设数列
上是否存在最小值,若存在,求该最小值;若不存在,说明理由;(3)设数列![]() 各项都是正数,且满足
各项都是正数,且满足![]() ,
,![]() (
(![]() ),又设
),又设![]() ,
,![]() ,
,![]() , 当
, 当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
(本题满分15分)设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() ”
”
(I)证明:函数![]() 是集合M中的元素;
是集合M中的元素;
(II)证明:函数![]() 具有下面的性质:对于任意
具有下面的性质:对于任意![]()
![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。
成立。
(III)若集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n]![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立。试用这一性质证明:对集合M中的任一元素
成立。试用这一性质证明:对集合M中的任一元素![]() ,方程
,方程![]() 只有一个实数根。
只有一个实数根。
(本题满分15分) 设函数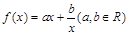 ,若
,若 在点
在点 处的切线斜率为
处的切线斜率为 .
.
(Ⅰ)用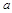 表示
表示 ;
;
(Ⅱ)设 ,若
,若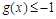 对定义域内的
对定义域内的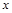 恒成立,
恒成立,
(ⅰ)求实数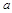 的取值范围;
的取值范围;
(ⅱ)对任意的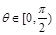 ,证明:
,证明: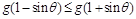 .
.
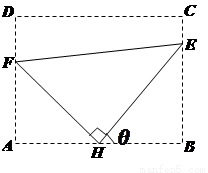
(本题满分15分)如图:某污水处理厂要在一个矩形污水处理池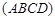 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道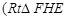 ,
,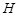 是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口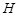 是
是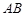 的中点,
的中点,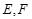 分别落在线段
分别落在线段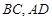 上.已知
上.已知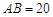 米,
米,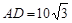 米,记
米,记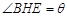 .
.
(Ⅰ)试将污水净化管道的长度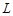 表示为
表示为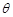 的函数
的函数
并写出定义域
(Ⅱ)若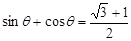 ,求此时管道的长度
,求此时管道的长度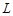
(Ⅲ)问:当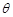 取何值时,铺设管道的成本最低?并求出此时管道的长度
取何值时,铺设管道的成本最低?并求出此时管道的长度
[来源:ZXXK]
 ,若
,若 在点
在点 处的切线斜率为
处的切线斜率为 .
. 表示
表示 ;
; ,若
,若 对定义域内的
对定义域内的 恒成立,
恒成立, 的取值范围;
的取值范围;  ,证明:
,证明: .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com