
题目列表(包括答案和解析)
(本题满分14分,第1小题满分7分,第2小题满分7分)
为了研究某种癌细胞的繁殖规律和一种新型抗癌药物的作用,将癌细胞注入一只小白鼠体内进行实验,经检测,癌细胞的繁殖规律与天数的关系如下表.已知这种癌细胞在小白鼠体内的个数超过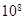 时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的
时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的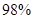 .
.
|
天数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
|
癌细胞个数 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
… |
(1)要使小白鼠在实验中不死亡,第一次最迟应在第几天注射该种药物?(精确到1天)
(2)若在第10天,第20天,第30天,……给小白鼠注射这种药物,问第38天小白鼠是否仍然存活?请说明理由.
(本题满分20分,其中第1小题4分,第2小题6分,第3小题10分)
已知![]() 是直线
是直线![]() 上的
上的![]() 个不同的点(
个不同的点(![]() ,
,![]() 、
、![]() 均为非零常数),其中数列
均为非零常数),其中数列![]() 为等差数列.
为等差数列.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求证:
,求证: ![]() ;
;
(3) 设![]() ,且当
,且当![]() 时,恒有
时,恒有![]() (
(![]() 和
和![]() 都是不大于
都是不大于![]() 的正整数, 且
的正整数, 且![]() ).试探索:在直线
).试探索:在直线![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 成立?请说明你的理由.
成立?请说明你的理由.
(本题满分14分,其中第1小题6分,第2小题8分)
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用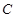 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度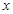 (单位:cm)满足关系:
(单位:cm)满足关系: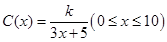 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设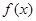 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求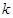 的值及
的值及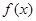 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用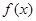 达到最小,并求最小值.
达到最小,并求最小值.
(本题满分16分)第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分6分。
 各项均为正数的数列
各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,数列
,数列![]() 满足
满足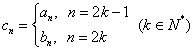 ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 为偶数时,求
为偶数时,求![]() ;
;
(3)若数列![]() ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的![]() ,试图确定
,试图确定![]() 的值是否可以等于20?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
的值是否可以等于20?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
(本小题满分12分) 第11届全国人大五次会议于20 1 2年3月5日至3月1 4日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和1 4名女记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语.
(Ⅰ)根据以上数据完成以下2×2列联表:
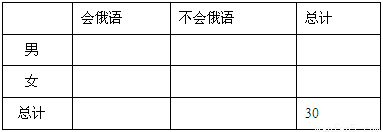
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
(参考公式: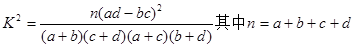
参考数据:

(Ⅱ)已知会俄语的6名女记者中有4人曾在俄罗斯工作过,若从会俄语的6名女记者中随
机抽取2人做同声翻译,则抽出的2人都在俄罗斯工作过的概率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com