如图12-3-3所示，一段横截面为正方形的玻璃棒，中间部分弯成四分之一圆弧形状，一细束单色光由MN端面的中点垂直射入，恰好能在弧面EF上发生全反射，然后垂直PQ端面射出．

图12-3-3

①求该玻璃棒的折射率．

②若将入射光向N端平移，当第一次射到弧面EF上时________(填“能”“不能”或“无法确定能否”)发生全反射．

解析　如图所示单色光照射到EF弧面上时刚好发

生全反射，由全反射的条件得C＝45°①

由折射定律得n＝②

联立①②式得n＝

答案　①　②能

已知氢原子基态的电子轨道半径r₁＝0.53×10^－10 m，基态的能级值为E₁＝－13.6 eV.

(1)求电子在n＝1的轨道上运动形成的等效电流．

(2)有一群氢原子处于量子数n＝3的激发态，画出能级图，在图上用箭头标明这些氢原子能发出哪几条光谱线．

(3)计算这几条光谱线中最长的波长．

【解析】：(1)电子绕核运动具有周期性，设运转周期为T，由牛顿第二定律和库仑定律有：k＝m²r₁①

又轨道上任一处，每一周期通过该处的电荷量为e，由电流的定义式得所求等效电流I＝②

联立①②式得

I＝

＝× A

＝1.05×10^－3 A

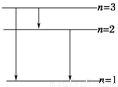
 (2)由于这群氢原子的自发跃迁辐射，会得到三条光谱线，如右图所示．

(3)三条光谱线中波长最长的光子能量最小，发生跃迁的两个能级的能量差最小，根据氢原子能级的分布规律可知，氢原子一定是从n＝3的能级跃迁到n＝2的能级

设波长为λ，由h＝E₃－E₂，得

λ＝

＝m

＝6.58×10^－7m

已知氢原子基态的电子轨道半径r₁＝0.53×10^－10 m，基态的能级值为E₁＝－13.6 eV.

(1)求电子在n＝1的轨道上运动形成的等效电流．

(2)有一群氢原子处于量子数n＝3的激发态，画出能级图，在图上用箭头标明这些氢原子能发出哪几条光谱线．

(3)计算这几条光谱线中最长的波长．

【解析】：(1)电子绕核运动具有周期性，设运转周期为T，由牛顿第二定律和库仑定律有：k＝m²r₁①

又轨道上任一处，每一周期通过该处的电荷量为e，由电流的定义式得所求等效电流I＝②

联立①②式得

I＝

＝× A

＝1.05×10^－3 A

 (2)由于这群氢原子的自发跃迁辐射，会得到三条光谱线，如右图所示．

(3)三条光谱线中波长最长的光子能量最小，发生跃迁的两个能级的能量差最小，根据氢原子能级的分布规律可知，氢原子一定是从n＝3的能级跃迁到n＝2的能级

设波长为λ，由h＝E₃－E₂，得

λ＝

＝m

＝6.58×10^－7m

两个质量分别为M₁和M₂的劈A和B，高度相同，放在光滑水平面上．A和B的倾斜面都是光滑曲面，曲面下端与水平面相切，如图17所示．一质量为m的物块位于劈A的倾斜面上，距水平面的高度为h.物块从静止开始滑下，然后又滑上劈B.求物块在B上能够达到的最大高度．

【解析】：设物块到达劈A的底端时，物块和A的速度大小分别为v和V，由机械能守恒和动量守恒得

mgh＝mv²＋M₁V²①

M₁V＝mv②

设物块在劈B上达到的最大高度为h′，此时物块和B的共同速度大小为V′，由机械能守恒和动量守恒得

mgh′＋(M₂＋m)V²＝mv²③

mv＝(M₂＋m)V′④

联立①②③④式得

h′＝h⑤

某同学利用如图所示的装置验证动量守恒定律．图中两摆摆长相同，悬挂于同一高度，A、B两摆球均很小，质量之比为1∶2.当两摆均处于自由静止状态时，其侧面刚好接触．向右上方拉动B球使其摆线伸直并与竖直方向成45°角，然后将其由静止释放．结果观察到两摆球粘在一起摆动，且最大摆角为30°.若本实验允许的最大误差为±4%，此实验是否成功地验证了动量守恒定律？

【解析】：设摆球A、B的质量分别为m_A、m_B，摆长为l，B球的初始高度h₁，碰撞前B球的速度为v_B.在不考虑摆线质量的情况下，根据题意及机械能守恒定律得h₁＝l(1－cos45°)①

m_Bv＝m_Bgh₁②

设碰撞前、后两摆球的总动量的大小分别为p₁、p₂，有

p₁＝m_Bv_B③

联立①②③式得p₁＝m_B④

同理可得p₂＝(m_B＋m_B)⑤

联立④⑤式得＝⑥

代入已知条件得()²＝1.03⑦

由此可以推出||≤4%⑧

所以，此实验在规定的范围内验证了动量守恒定律．