
题目列表(包括答案和解析)
若定义在 上的函数
上的函数 满足条件:存在实数
满足条件:存在实数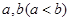 且
且

 ,使得:
,使得:
⑴ 任取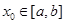 ,有
,有 (
( 是常数);
是常数);
⑵ 对于 内任意
内任意 ,当
,当 ,总有
,总有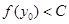 。
。
我们将满足上述两条件的函数 称为“平顶型”函数,称
称为“平顶型”函数,称 为“平顶高度”,称
为“平顶高度”,称 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题:
(1)函数 是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
(2) 已知 是“平顶型”函数,求出
是“平顶型”函数,求出 的值。
的值。
(3)对于(2)中的函数 ,若
,若 在
在 上有两个不相等的根,求实数
上有两个不相等的根,求实数 的取值范围。
的取值范围。
若定义在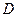 上的函数
上的函数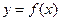
 满足条件:存在实数
满足条件:存在实数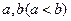 且
且

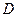 ,使得:
,使得:
⑴ 任取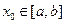 ,有
,有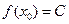 (
(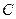 是常数);
是常数);
⑵ 对于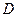 内任意
内任意 ,当
,当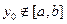 ,总有
,总有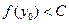 。
。
我们将满足上述两条件的函数 称为“平顶型”函数,称
称为“平顶型”函数,称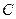 为“平顶高度”,称
为“平顶高度”,称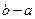 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题:
(1)函数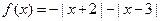 是否为“平顶型”函
是否为“平顶型”函 数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
(2) 已知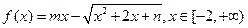 是“平顶型”函数,求出
是“平顶型”函数,求出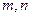 的值。
的值。
(3)对于(2)中的函数 ,若
,若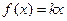 在
在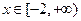 上有两个不相等的根,求实数
上有两个不相等的根,求实数 的取值范围。
的取值范围。
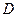 上的函数
上的函数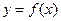
 满足条件:存在实数
满足条件:存在实数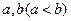 且
且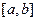

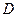 ,使得:
,使得: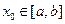 ,有
,有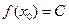 (
(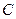 是常数);
是常数);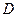 内任意
内任意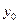 ,当
,当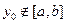 ,总有
,总有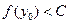 。
。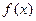 称为“平顶型”函数,称
称为“平顶型”函数,称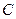 为“平顶高度”,称
为“平顶高度”,称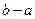 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题: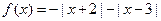 是否为“平顶型”函
是否为“平顶型”函 数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。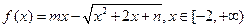 是“平顶型”函数,求出
是“平顶型”函数,求出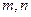 的值。
的值。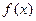 ,若
,若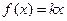 在
在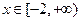 上有两个不相等的根,求实数
上有两个不相等的根,求实数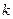 的取值范围。
的取值范围。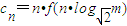 (n∈N*),问是否存在正实数m,使得数列{cn}是单调递减数列?若存在,求出m的取值范围;若不存在,请说明理由.
(n∈N*),问是否存在正实数m,使得数列{cn}是单调递减数列?若存在,求出m的取值范围;若不存在,请说明理由.| x2+2x+n |
13. 8 ; 14. 卷.files/image035.gif) ; 15.
; 15.卷.files/image280.gif) ;16.①③
;16.①③
17.解:(1)解:在卷.files/image182.gif) 中
中 卷.files/image283.gif)
卷.files/image285.gif)
卷.files/image287.gif) 2分
2分
卷.files/image289.gif)
卷.files/image287.gif) 4分
4分
卷.files/image291.gif)
卷.files/image293.gif)
卷.files/image295.gif)
卷.files/image297.gif)
卷.files/image287.gif) 6分
6分
(2)卷.files/image188.gif) =
=卷.files/image299.gif)
卷.files/image287.gif) 10分
10分
18(1)解:设从A中任取一个元素是卷.files/image209.gif) 的事件为B
的事件为B
P(B)=卷.files/image301.gif)
所以从A中任取一个元素是卷.files/image209.gif) 的概率为
的概率为卷.files/image301.gif)
卷.files/image287.gif) 3分
3分
(2)设从A中任取一个元素,卷.files/image211.gif) 的事件为C 有
的事件为C 有
(4,6)(6,4)(5,5)(5,6)(6,5)(6,6)
P(C)=卷.files/image303.gif)
所以从A中任取一个元素卷.files/image211.gif) 的概率为
的概率为卷.files/image303.gif)
卷.files/image287.gif) 6分
6分
(3)卷.files/image213.gif) 可能取的值为2,3,4,5,6,7,8,9,10,11,12
可能取的值为2,3,4,5,6,7,8,9,10,11,12 卷.files/image287.gif) 8分
8分
卷.files/image306.gif)
卷.files/image308.gif)
卷.files/image310.gif)
卷.files/image312.gif)
卷.files/image314.gif)
卷.files/image316.gif)
卷.files/image318.gif)
卷.files/image320.gif)
卷.files/image322.gif)
卷.files/image324.gif)
卷.files/image326.gif)
卷.files/image213.gif)
2
3
4
5
6
7
8
9
10
11
12
卷.files/image329.gif)
卷.files/image301.gif)
卷.files/image331.gif)
卷.files/image333.gif)
卷.files/image335.gif)
卷.files/image337.gif)
卷.files/image339.gif)
卷.files/image337.gif)
卷.files/image335.gif)
卷.files/image333.gif)
卷.files/image331.gif)
卷.files/image301.gif)
卷.files/image287.gif) 10分
10分
卷.files/image341.gif) =7
=7
卷.files/image287.gif) 12分
12分
19. 解:(1)卷.files/image343.gif)
卷.files/image199.gif) ,
,卷.files/image197.gif)
卷.files/image345.gif)
卷.files/image347.gif) 又
又卷.files/image195.gif)
卷.files/image349.gif)
卷.files/image351.gif) ,又
,又卷.files/image353.gif)
卷.files/image355.gif)
卷.files/image357.gif) 面PAB,
面PAB,卷.files/image359.gif) 面PAB,
面PAB,卷.files/image361.gif)
卷.files/image363.gif)
卷.files/image287.gif) 4分
4分
(2)过B点作BF卷.files/image203.gif) AD于F,过F作FM
AD于F,过F作FM卷.files/image203.gif) PD于M,联结BM
PD于M,联结BM
卷.files/image366.gif) BF
BF卷.files/image203.gif) AD
AD
BF卷.files/image203.gif) PA
PA 卷.files/image368.gif) BF
BF卷.files/image203.gif) 面PAD
面PAD
BM为面PAD的斜线,MF为BM在面PAD的射影,卷.files/image368.gif) BM
BM卷.files/image203.gif) PD
PD
卷.files/image370.gif) BMF为二面角B-PD-A的平面角
BMF为二面角B-PD-A的平面角
卷.files/image287.gif) 8分
8分
PC与面ABCD成角卷.files/image372.gif) ,
,卷.files/image370.gif) PCA=
PCA=卷.files/image372.gif) PA=3
PA=3
BF=卷.files/image374.gif) MF=
MF=卷.files/image376.gif)
卷.files/image378.gif)
所以二面角B-PD-A为卷.files/image380.gif)
卷.files/image287.gif) 12分
12分
20. 解(1)卷.files/image366.gif)
卷.files/image229.gif)
卷.files/image368.gif)
卷.files/image385.gif)
卷.files/image387.gif)
卷.files/image389.gif)
卷.files/image391.gif)
卷.files/image368.gif)
卷.files/image394.gif) 为等差数列
为等差数列 卷.files/image287.gif) 6分
6分
(2)卷.files/image396.gif)
卷.files/image398.gif)
卷.files/image287.gif) 12分
12分
21. 解:(1)卷.files/image400.gif)
卷.files/image402.gif)
卷.files/image287.gif) 2分
2分
x
(-卷.files/image404.gif) ,-3)
,-3)
-3
(-3,1)
1
(1,+卷.files/image404.gif) )
)
卷.files/image407.gif)
+
0
-
0
+
卷.files/image409.gif) (x)
(x)
增
极大值
减
极小值
增
卷.files/image411.gif)
卷.files/image287.gif) 4分
4分
(2)卷.files/image413.gif)
卷.files/image415.gif)
卷.files/image417.gif)
卷.files/image419.gif)
卷.files/image421.gif)
卷.files/image423.gif)
卷.files/image425.gif)
卷.files/image427.gif)
卷.files/image287.gif) 7分
7分
卷.files/image366.gif) 3
3卷.files/image249.gif) 恒成立
恒成立
卷.files/image368.gif) 3
3卷.files/image431.gif) 恒成立
恒成立
卷.files/image368.gif)
卷.files/image433.gif) 恒成立
恒成立
卷.files/image368.gif)
卷.files/image435.gif)
卷.files/image437.gif)
卷.files/image439.gif)
卷.files/image441.gif)
卷.files/image287.gif) 12分
12分
22. 解:(I)卷.files/image443.gif) ,
,卷.files/image445.gif)
所以卷.files/image447.gif) 为线段
为线段卷.files/image257.gif) 的垂直平分线,
的垂直平分线,卷.files/image450.gif)
卷.files/image452.gif)
所以动点卷.files/image259.gif) 的轨迹是以
的轨迹是以卷.files/image455.gif) ,
,卷.files/image457.gif) 为焦点的椭圆,且长轴长为
为焦点的椭圆,且长轴长为卷.files/image459.gif) ,焦距
,焦距卷.files/image461.gif) ,所以
,所以卷.files/image463.gif) ,
,卷.files/image465.gif) ,
,卷.files/image467.gif)
曲线E的方程为卷.files/image469.gif) .
.
卷.files/image287.gif) 4分
4分
(II)(2)设F(x1,y1)H(x2,y2),则由卷.files/image471.gif) ,
,
消去y得卷.files/image473.gif)
卷.files/image475.gif)
卷.files/image477.gif)
卷.files/image479.gif)
卷.files/image287.gif) 8分
8分
卷.files/image481.gif)
又点卷.files/image087.gif) 到直线
到直线卷.files/image484.gif) 的距离
的距离卷.files/image486.gif) ,
,
卷.files/image488.gif)
卷.files/image490.gif)
卷.files/image492.gif)
卷.files/image494.gif)
卷.files/image496.gif)
卷.files/image287.gif) 12分
12分
www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com