
题目列表(包括答案和解析)
造船厂年造船量20艘,造船![]() 艘产值函数为
艘产值函数为![]() (单位:万元),成本函数
(单位:万元),成本函数![]() (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]()
(1)求利润函数![]() 及边际利润函数
及边际利润函数![]() (利润=产值—成本)
(利润=产值—成本)
(2)问年造船量安排多少艘时,公司造船利润最大
(3)边际利润函数![]()
![]() 的单调递减区间
的单调递减区间
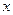 艘产值函数为
艘产值函数为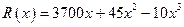 (单位:万元),成本函数
(单位:万元),成本函数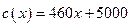 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数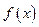 的边际函数
的边际函数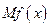 定义为
定义为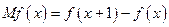
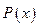 及边际利润函数
及边际利润函数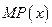 (利润=产值—成本)
(利润=产值—成本)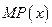
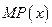 的单调递减区间
的单调递减区间某造船公司年最高造船量是20艘. 已知造船x艘的产值函数R (x)=3700x + 45x2 – 10x3(单位:万元), 成本函数为C (x) = 460x + 5000 (单位:万元). 又在经济学中,函数f(x)的边际函数Mf (x)定义为: Mf (x) = f (x+1) – f (x). 求:(提示:利润 = 产值 – 成本)
(1) 利润函数P(x) 及边际利润函数MP(x);
(2) 年造船量安排多少艘时, 可使公司造船的年利润最大?
(3) 边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?
某造船公司年造船量是20艘,已知造船![]() 艘的产值函数为
艘的产值函数为![]() (单位:万元),成本函数为
(单位:万元),成本函数为![]() (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() 。
。
(Ⅰ)求利润函数![]() 及边际利润函数
及边际利润函数![]() ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数![]() 单调递减时
单调递减时![]() 的取值范围。
的取值范围。
(本小题12分)
某造船公司年造船量是20艘,已知造船 艘的产值函数为
艘的产值函数为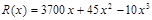 (单位:万元),成本函数为
(单位:万元),成本函数为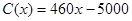 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数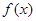 的边际函数
的边际函数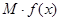 定义为
定义为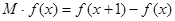 。
。
(Ⅰ)求利润函数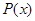 及边际利润函数
及边际利润函数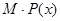 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数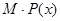 单调递减时
单调递减时 的取值范围。
的取值范围。
一.选择题(本大题共10小题,每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
C
B
C
A
B
D
A
B
二.填空题(本大题共5小题,满分20分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image252.gif) 则
则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image254.gif) >0 ; 100.5000;
>0 ; 100.5000; /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image045.gif) ;
; /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image257.gif) ;
; /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image259.gif)
三.解答题(本大题共6小题,共80分)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image139.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image140.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image140.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image139.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image139.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image140.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image139.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image140.gif)
16.(本小题满分12分)
(Ⅰ)解:由余弦定理,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image261.gif) =
=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image043.gif) (2分) ∵
(2分) ∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image264.gif) ,∴
,∴
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image266.gif) .(4分)
.(4分)
(Ⅱ)解法一:将/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image158.gif) 代入
代入/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image154.gif) ,得
,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image268.gif) .
……6分
.
……6分
由余弦定理,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image270.gif) .
……8分
.
……8分
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image272.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image274.gif) .(10分) ∴
.(10分) ∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image276.gif) .(12分)
.(12分)
解法二:将/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image158.gif) 代入
代入/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image154.gif) ,得
,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image268.gif) .
……6分
.
……6分
由正弦定理,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image278.gif) .(8分)
∵
.(8分)
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image266.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image280.gif) .(10分)
.(10分)
又/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image282.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image284.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image286.gif) 。 ∴
。 ∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image276.gif) .(12分)
.(12分)
解法三:∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image158.gif) ,
由正弦定理,得
,
由正弦定理,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image288.gif) .
……6分
.
……6分
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image266.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image290.gif) . ∴
. ∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image292.gif) .……8分
.……8分
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image294.gif) .∴
.∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image296.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image139.gif) ……10分
……10分
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image276.gif) .
……12分
.
……12分
17.(本小题满分14分)
解法一:(1)连接BD,由已知有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image298.gif) 得
得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image300.gif) …………………………………1分
…………………………………1分
又由ABCD是正方形,得:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image302.gif) ……2分
∵
……2分
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image304.gif) 与
与/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image306.gif) 相交,∴
相交,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image308.gif) ……3分
……3分
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image310.gif) (2)延长DC至G,使CG=EB,,连结BG.D
(2)延长DC至G,使CG=EB,,连结BG.D
∴BG∥EC.∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image312.gif) 就是异面直线BD1与CE所成角…………………………5分
就是异面直线BD1与CE所成角…………………………5分
在/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image314.gif) 中,
中,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image316.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image318.gif) …………………6分
…………………6分
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image320.gif) 异面直线
异面直线
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image324.gif) 与CE所成角的余弦值是
与CE所成角的余弦值是/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image326.gif) ……………………………8分
……………………………8分
(3)∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image328.gif) ∴
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image330.gif) 又∵
又∵/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image332.gif) ∴
点E到
∴
点E到/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image334.gif) 的距离
的距离/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image336.gif) ,有:
,有:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image338.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image340.gif) ,…………11分
,…………11分
又由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image342.gif) , 设点B到平面
, 设点B到平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image176.gif) 的距离为
的距离为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image344.gif) ,
,
则/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image346.gif) ,
有
,
有/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image348.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image350.gif) ,
所以点B到平面
,
所以点B到平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image176.gif) 的距离为
的距离为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image352.gif) …14分
…14分
解法二:(1)见解法一…………………………3分
(2)以D为原点,DA.DC./file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image354.gif) 为
为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image356.gif) 轴建立空间直角坐标系,则有B(2,2,0).
轴建立空间直角坐标系,则有B(2,2,0)./file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image357.gif) (0,0,2).E(2,1,0).C(0,2,0).
(0,0,2).E(2,1,0).C(0,2,0)./file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image359.gif) (2,0,2)∴
(2,0,2)∴/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image361.gif) (-2,-2,2),
(-2,-2,2),/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image363.gif) (2,-1,0)………5分
(2,-1,0)………5分
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image365.gif) ……7分 即……余弦值是
……7分 即……余弦值是/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image326.gif) ……8分
……8分
(3)设平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image176.gif) 的法向量为
的法向量为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image368.gif) ,
有:
,
有:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image370.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image372.gif) ,…………8分
,…………8分
由:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image374.gif) (0,1,-2),
(0,1,-2),/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image363.gif) (2,-1,0)…………………………9分
(2,-1,0)…………………………9分
可得:/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image376.gif) ,令
,令/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image378.gif) ,得
,得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image380.gif) …………………………11分
…………………………11分
由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image382.gif) (0,1,0) 有:点B到平面
(0,1,0) 有:点B到平面/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image176.gif) 的距离为
的距离为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image384.gif) ………………14分
………………14分
18.(本小题满分14分)
解:(Ⅰ)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image386.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image388.gif) ; 2分
; 2分
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image390.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image392.gif) .…………… 4分
.…………… 4分
(Ⅱ)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image394.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image396.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image398.gif)
即年造船量安排12 艘时,可使公司造船的年利润最大. ……………………8分
(Ⅲ)/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image400.gif) ……………………11分
……………………11分
所以,当/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image402.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image192.gif) 单调递减,
单调递减,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image194.gif) 的取值范围为
的取值范围为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image405.gif) ,且
,且/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image407.gif) …………12分
…………12分
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image192.gif) 是减函数的实际意义:随着产量的增加,每艘船的利润在减少.14分
是减函数的实际意义:随着产量的增加,每艘船的利润在减少.14分
19.(本小题满分12分)
解:(Ⅰ)依题意,甲答对试题数ξ的可能取值为0.1.2.3,则
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image410.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image412.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image414.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image416.gif) (4分)
(4分)
ξ
0
1
2
3
P
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image418.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image420.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image422.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image424.gif)
其分布列如下:
甲答对试题数ξ的数学期望:
Eξ=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image426.gif) .…………6分
.…………6分
(Ⅱ)设甲.乙两人考试合格的事件分别为A.B,则
P(A)=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image428.gif) =
=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image430.gif) , P(B)=
, P(B)=/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image432.gif) .………9分
.………9分
因为事件A.B相互独立,
∴甲.乙两人考试均不合格的概率为 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image434.gif) ,
,
∴甲.乙两人至少有一人考试合格的概率为 /file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image436.gif) .
.
答:甲.乙两人至少有一人考试合格的概率为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image438.gif) .
…………………12分
.
…………………12分
另解:甲.乙两人至少有一个考试合格的概率为(三种情况两两互斥.A.B相互独立)
/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image440.gif) .
.
答:甲.乙两人至少有一人考试合格的概率为/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image438.gif) .
.
20.(本小题满分14分)
解:(1)由/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image443.gif) 又由已知得
又由已知得/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image445.gif) 2分
2分
故/file:///E:\cooco.net.cn\docfiles\down\test\down\%25&Ovr0\ba99990fec167491b5d396ac32758af9.zip\65006\福建福州八中2009年元月高三调研考试试卷(全套六科)\福建福州八中2009年元月高三调研考试试卷(数学理).files\image447.gif)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com