
题目列表(包括答案和解析)
设定义在[0,2]上的函数![]() 满足下列条件:
满足下列条件:
①对于![]() ,总有
,总有![]() ,且
,且![]() ,
,![]() ;
;
②对于![]() ,若
,若![]() ,则
,则![]() .
.
证明:(1)![]() (
(![]() );(2)
);(2)![]() 时,
时,![]() .
.
设定义在[0,2]上的函数![]() 满足下列条件:
满足下列条件:
①对于![]() ,总有
,总有![]() ,且
,且![]() ,
,![]() ;
;
②对于![]() ,若
,若![]() ,则
,则![]() .
.
证明:(1)![]() (
(![]() );(2)
);(2)![]() 时,
时,![]() .
.
设定义在[0,2]上的函数![]() 满足下列条件:
满足下列条件:
①对于![]() ,总有
,总有![]() ,且
,且![]() ,
,![]() ;
;
②对于![]() ,若
,若![]() ,则
,则![]() .
.
证明:(1)![]() (
(![]() );(2)
);(2)![]() 时,
时,![]() .
.
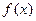 满足下列条件:
满足下列条件: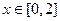 ,总有
,总有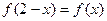 ,且
,且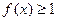 ,
,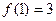 ;
;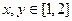 ,若
,若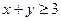 ,则
,则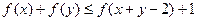 .
.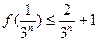 (
(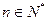 );(2)
);(2)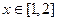 时,
时,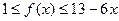 .
.| 1 |
| 3n |
| 2 |
| 3n |
一、 选择题(本大题共6小题,每小题6分,满分36分)
1.函数 的图像过点(-1,3),则函数
的图像过点(-1,3),则函数 的图像关于
的图像关于 轴对称的图形一定过点( ).
轴对称的图形一定过点( ).
A (1,-3) B (-1,3) C (-3,-3) D (-3,3)
答案:B.
2.把2008表示成两个整数的平方差形式,则不同的表示方法有( )种.
A 4
B
答案:C.
解: 设 ,即
,即 .2008有8个正因数,分别为1,2,4,8,251,502,1004,2008.而且
.2008有8个正因数,分别为1,2,4,8,251,502,1004,2008.而且 与
与 只能同为偶数,因此对应的方程组为
只能同为偶数,因此对应的方程组为

故 共有8组不同的值:
共有8组不同的值: ;
; .
.
3.若函数 有最小值,则a的取值范围是( ).
有最小值,则a的取值范围是( ).
A  B
B  C
C  D
D 
答案:C.
解:当 时,
时, 是递减函数,由于
是递减函数,由于 没有最大值,所以
没有最大值,所以 没有最小值;当
没有最小值;当 时,
时, 有最小值等价于
有最小值等价于 有大于0的最小值.这等价于
有大于0的最小值.这等价于 ,因此
,因此 .
.
4.已知 则
则 的最小值是( ).
的最小值是( ).
A  B
B
 C
2
D 1
C
2
D 1
答案:A.
解:记 ,则
,则 ,
,
 ,(当且仅当
,(当且仅当 时取等号).故选A.
时取等号).故选A.
5.已知 ,则
,则 的取值范围是( ).
的取值范围是( ).
A  B
B  C
C  D
D 
答案:D.
解:设 ,易得
,易得 ,即
,即 .由于
.由于 ,所以
,所以 ,解得
,解得  .
.
6.函数 是
是 上的单调递增函数,当
上的单调递增函数,当 时,
时, ,且
,且 ,则
,则 的值等于( ).
的值等于( ).
A 1 B
答案:B
解:(用排除法)令 ,则得
,则得 .
.
若 ,则
,则 ,与
,与 矛盾;
矛盾;
若 ,则
,则 ,与“
,与“ 在
在 上单调递增”矛盾;
上单调递增”矛盾;
若 ,则
,则 ,也与“
,也与“ 在
在 上单调递增”矛盾.
上单调递增”矛盾.
故选B.
二、填空题(本大题共6小题,每小题9分,满分54分)
7.设集合 ,
, 是S的子集,且
是S的子集,且 满足:
满足: ,
, ,那么满足条件的子集的个数为 .
,那么满足条件的子集的个数为 .
答案:371.
解:当 时,
时, 有
有 种选择方法,
种选择方法,  有6种选择方法,所以
有6种选择方法,所以 共有
共有 种选择方法;当
种选择方法;当 时,一旦
时,一旦 取定,
取定, 有
有 种选择方法,
种选择方法, 有
有 种选择方法,所以选择
种选择方法,所以选择 的方法有
的方法有  种.
种.
综上,满足条件的子集共有371个.
8.已知数列 满足
满足
 ,则
,则 =___ .
=___ .
答案: .
.
解:由已知得 ,且
,且 .
.
所以 ,即{
,即{ }是首项、公差均为1的等差数列,所以
}是首项、公差均为1的等差数列,所以 =n,即有
=n,即有 .
.
9.已知坐标平面上三点 ,
, 是坐标平面上的点,且
是坐标平面上的点,且 ,则
,则 点的轨迹方程为
.
点的轨迹方程为
.
答案: .
.
 解:如图,作正三角形
解:如图,作正三角形 ,由于
,由于 也是正三角形,所以可证得
也是正三角形,所以可证得  ≌
≌ ,所以
,所以 .
.
又因为 ,所以点
,所以点 共线.
共线.
 ,所以P点在
,所以P点在 的外接圆上,又因为
的外接圆上,又因为 ,所以所求的轨迹方程为
,所以所求的轨迹方程为
 .
.
10. 在三棱锥 中,
中, ,
, ,
, ,
, ,
, ,
, .则三棱锥
.则三棱锥 体积的最大值为
.
体积的最大值为
.
答案: .
.
解:设 ,根据余弦定理有
,根据余弦定理有 ,
,
故 ,
, .由于棱锥的高不超过它的侧棱长,所以
.由于棱锥的高不超过它的侧棱长,所以 .事实上,取
.事实上,取 ,
, 且
且 时,可以验证满足已知条件,此时
时,可以验证满足已知条件,此时 ,棱锥的体积可以达到最大.
,棱锥的体积可以达到最大.
11. 从m个男生,n个女生( )中任选2个人当组长,假设事件A表示选出的2个人性别相同,事件B表示选出的2个人性别不同.如果A的概率和B的概率相等,则(m,n)的可能值为 .
)中任选2个人当组长,假设事件A表示选出的2个人性别相同,事件B表示选出的2个人性别不同.如果A的概率和B的概率相等,则(m,n)的可能值为 .
答案:(10,6).
解: ,由于
,由于 ,所以
,所以 ,整理得
,整理得 .即
.即 是完全平方数,且
是完全平方数,且 ,因此
,因此
 ,
, ,解得
,解得  (不合条件),
(不合条件), .
.
所以 .
.
12. 是平面上不共线三点,向量
是平面上不共线三点,向量 ,
, ,设P为线段AB垂直平分线上任意一点,向量
,设P为线段AB垂直平分线上任意一点,向量 .若
.若 ,
, ,则
,则 的值是
____
____.
的值是
____
____.
答案:8.
 解:如图,
解:如图, 是线段AB的垂直平分线,
是线段AB的垂直平分线, ,
,
 ,
, ,
,

 .
.
三、解答题(本大题共5小题,每题的解答均要求有推理过程,13小题10分,17小题14分,其余每小题12分,满分60分)
13. 是两个不相等的正数,且满足
是两个不相等的正数,且满足 ,求所有可能的整数c,使得
,求所有可能的整数c,使得 .
.
解:由 得
得 ,所以
,所以 ,
,
由此得到 .
.
又因为 ,故
,故 .………………………4分
.………………………4分
又因为 , 令
, 令  则
则 .……………6分
.……………6分
当 时,
时, 关于t单调递增,所以
关于t单调递增,所以 ,
, .
.
因此  可以取1,2,3. …………………………………………………………………10分
可以取1,2,3. …………………………………………………………………10分
 14.如图,斜三棱柱
14.如图,斜三棱柱 的所有棱长均为
的所有棱长均为 ,侧面
,侧面 底面
底面 ,且
,且 .
.
(1) 求异面直线 与
与 间的距离;
间的距离;
(2) 求侧面 与底面
与底面 所成二面角的度数.
所成二面角的度数.
 解:(1)如图,取
解:(1)如图,取 中点D,连
中点D,连 .
.
 .
.
 ,
,
∴ .
.
由 .……………4分
.……………4分
 ∥
∥ 
 ∥平面
∥平面 .
.
所以异面直线 与
与 间的距离等于
间的距离等于
 .……………6分
.……………6分
(2)如图,

 ………………………………..……8分
………………………………..……8分
 .……………………12分
.……………………12分
15.设向量 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com