
题目列表(包括答案和解析)
| 分数段 | [29~40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 午休考生 人数 |
23 | 47 | 30 | 21 | 14 | 31 | 14 |
| 不午休考 生人数 |
17 | 51 | 67 | 15 | 30 | 17 | 3 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| 及格人数 | 不及格人数 | 总计 | |
| 午休 | |||
| 不午休 | |||
| 总计 |
20.在二项式 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列
(1)求展开式的常数项; (2)求展开式中二项式系数最大的项;
(3)求展开式中各项的系数和。
【解析】本试题主要考查了二项式定理中通项公式和二项式系数的概念以及求解各个系数和的运用,赋值法思想要深刻体会。
(本题满分12分)已知函数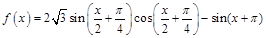 。
。
(1)求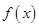 的最小正周期;
的最小正周期;
(2)若将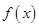 的图象向右平移
的图象向右平移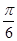 个单位,得到函数
个单位,得到函数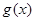 的图象,求函数
的图象,求函数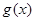 在区间
在区间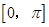 上的最大值和最小值。
上的最大值和最小值。
【解析】第一问中主要利用三角函数的两角和差公式化简为单一三角函数解析式
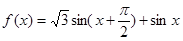 =
=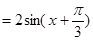
然后利用周期公式得到第一问。
第二问中,由于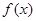 的图象向右平移
的图象向右平移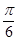 个单位,得到函数
个单位,得到函数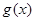 的图象,
的图象,
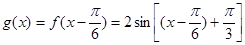
然后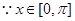 时,
时,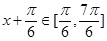 结合三角函数值域求解得到范围。
结合三角函数值域求解得到范围。
已知在△ABC中,角A、B、C所对的边分别为a,b,c,且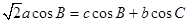 。
。
(1)求角B的大小;
(2)设向量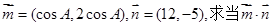 取最大值时,tanC的值。
取最大值时,tanC的值。
【解析】本试题主要是考查了解三角形中正弦定理的运用,先求解B,然后,利用数量积公式我们表示向量积,从而借助于三角形中值域来求解C的正切值。
在△ABC中,角A,B,C所对的边分别为a,b,c, △ABC的面积
S=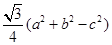
(1)求角C的大小
(2)若c=1,求△ABC周长L的取值范围
【解析】本试题主要是考查了解三角形中的面积公式和两个定理的运用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com