
题目列表(包括答案和解析)
(本小题16分)已知数列![]() 的前n项的和Sn,满足
的前n项的和Sn,满足![]() .
.
(1)求数列![]() 的通项公式.(2)设
的通项公式.(2)设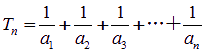 ,是否存在正整数k,使得当n≥3时,
,是否存在正整数k,使得当n≥3时,![]() 如果存在,求出k;如果不存在,请说明理由.
如果存在,求出k;如果不存在,请说明理由.
(本小题16分)
已知抛物线的顶点在坐标原点,对称轴为 轴,焦点
轴,焦点 在直线
在直线 上,直线
上,直线 与抛物线相交于
与抛物线相交于 两点,
两点, 为抛物线上一动点(不同于
为抛物线上一动点(不同于 ),直线
),直线 分别交该抛物线的准线
分别交该抛物线的准线 于点
于点 。
。
(1)求抛物线方程;
(2)求证:以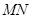 为直径的圆
为直径的圆 经过焦点
经过焦点 ,且当
,且当 为抛物线的顶点时,圆
为抛物线的顶点时,圆 与直线
与直线 相切。
相切。

(本小题16分)
已知△OAB的顶点坐标为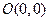 ,
,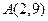 ,
,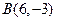 , 点P的横坐标为14,且
, 点P的横坐标为14,且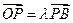 ,点
,点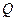 是边
是边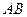 上一点,且
上一点,且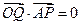 .
.
(1)求实数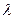 的值与点
的值与点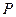 的坐标;
的坐标;
(2)求点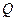 的坐标;
的坐标;
(3)若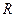 为线段
为线段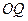 上的一个动点,试求
上的一个动点,试求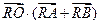 的取值范围.
的取值范围.
(本小题16分)
首项为正数的数列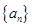 满足
满足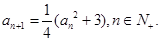
(I)证明:若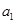 为奇数,则对一切
为奇数,则对一切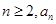 都是奇数;
都是奇数;
(II)若对一切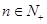 都有
都有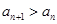 ,求
,求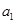 的取值范围.
的取值范围.
(本小题16分)
已知![]() 是定义在
是定义在![]() 上的偶函数,且
上的偶函数,且![]() 时,
时,![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求函数![]() 的表达式;
的表达式;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
1、 2、充分不必要;3、
2、充分不必要;3、 ;4、73;5、8;6、5049;
;4、73;5、8;6、5049;
7、1;8、 ;9、
;9、 ;10、
;10、 ;11、圆内;12、
;11、圆内;12、 ;
;
13、 ;14、
;14、
15、解:(Ⅰ)设区域A中任意一点P
 为事件M.?????????????????????????????????????? 1分
为事件M.?????????????????????????????????????? 1分
因为区域A的面积为 ,区域B在区域A的面积为
,区域B在区域A的面积为 ,????????????????????? 5分
,????????????????????? 5分
故 .??????????????????????????????????????????????????????????????????????????????????????????? 7分
.??????????????????????????????????????????????????????????????????????????????????????????? 7分
(Ⅱ)设点P 在集合B为事件N,????????????????????????????????????????????????????????????? 8分
在集合B为事件N,????????????????????????????????????????????????????????????? 8分
甲、乙两人各掷一次骰子所得的点P 的个数为36个,其中在区域B中的点P
的个数为36个,其中在区域B中的点P 有21个. 12分
有21个. 12分
故 .
.
16、解:(1)因为 边所在直线的方程为
边所在直线的方程为 ,且
,且 与
与 垂直,所以直线
垂直,所以直线 的斜率为
的斜率为 .………………………………………3分
.………………………………………3分
又因为点 在直线
在直线 上,所以
上,所以 边所在直线的方程为即
边所在直线的方程为即 . ………………………………………7分
. ………………………………………7分
(2)由 解得点
解得点 的坐标为
的坐标为 ,因为矩形
,因为矩形 两条对角线的交点为
两条对角线的交点为 .所以
.所以 为矩形
为矩形 外接圆的圆心.又
外接圆的圆心.又 .从而矩形
.从而矩形 外接圆的方程为
外接圆的方程为 .…………………………………14分
.…………………………………14分
17、证明:(Ⅰ)在 中,
中,
∵ ,
, ,
, ,∴
,∴ .
.
 ∴
∴ .----------------2分
.----------------2分
又 ∵平面 平面
平面 ,
,
平面 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .
.
又 平面
平面 ,∴平面
,∴平面 平面
平面 .----------4分
.----------4分
(Ⅱ)当 点位于线段PC靠近C点的三等分点
点位于线段PC靠近C点的三等分点
处时, 平面
平面 .--------5分
.--------5分
证明如下:连接AC,交 于点N,连接MN.
于点N,连接MN.
∵ ,所以四边形
,所以四边形 是梯形.
是梯形.
∵ ,∴
,∴ .
.
又 ∵ ,
,
∴
 ,∴
,∴ MN.????????????????????????????????????????????????????????????? 7分
MN.????????????????????????????????????????????????????????????? 7分
∵ 平面
平面 ,∴
,∴ 平面
平面 .??????????????????????????????????????????????????????? 9分
.??????????????????????????????????????????????????????? 9分
(Ⅲ)过 作
作 交
交 于
于 ,
,
∵平面 平面
平面 ,
,
∴ 平面
平面 .
.
即 为四棱锥
为四棱锥 的高.??????????????????????????????????????????????????????????????????? 11分
的高.??????????????????????????????????????????????????????????????????? 11分
又 ∵ 是边长为4的等边三角形,∴
是边长为4的等边三角形,∴ .??????????????????? 12分
.??????????????????? 12分
在 中,斜边
中,斜边 边上的高为
边上的高为 ,此即为梯形
,此即为梯形 的高.
的高.
∴梯形 的面积
的面积 .????????????????????????????????????????? 14分
.????????????????????????????????????????? 14分
故 .
.
18、解:(1)由 ,得
,得
 ,…………………………2分
,…………………………2分
 ,
,
 ,
,  ,
,
于是 ,
,  ,
,
∴ ,即
,即
 .…………………………7分
.…………………………7分
(2)∵ 角是一个三角形的最小内角,∴0<
角是一个三角形的最小内角,∴0< ≤
≤ ,
, ,………………10分
,………………10分
设 ,则
,则 ≥
≥ (当且仅当
(当且仅当 时取=),………12分
时取=),………12分
故函数 的值域为
的值域为 .…
.…
19、解:(1)2008年A型车价格为32+32×25%=40(万元)
设B型车每年下降d万元,2003,2003,…,2008年B型车价格分别为 …,
…, 为公差是-d的等差数列)
为公差是-d的等差数列)

即

故每年至少下降2万元。
(2)2008年到期时共有钱33
 (万元)
(万元)
故5年到期后这笔钱够买一辆降价后的B型车。
20、(I)由已知,可得 ,
, ,1分
,1分
∴ 解之得
解之得 ,
, 3分
3分
 4分
4分
(II)
 5分
5分

= 8分
8分
(III)
 10分
10分
 (1)
(1)
 (2)
(2)
(1)―(2)得:

 =
= ,即
,即 ,当
,当 时,
时, ,13分
,13分
 ,使得当
,使得当 时,
时,
 恒成立 14分
恒成立 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com