
题目列表(包括答案和解析)
 在三棱柱ABC-A1B1C1中,∠ACB=120°,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合).过D1和CC1的平面与AB交于D.
在三棱柱ABC-A1B1C1中,∠ACB=120°,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合).过D1和CC1的平面与AB交于D.
| ||
| 3 |
| 2 |
| CF |
| FB |
如图,在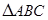 中,
中,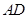 为
为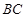 边上的中线,
边上的中线,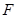 为
为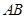 上任意一点,
上任意一点,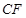 交
交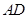 于点
于点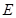 .求证:
.求证: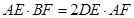 .
.
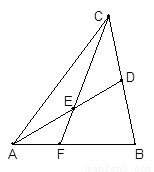
【解析】本试题主要是考查了平面几何中相似三角形性质的运用。根据已知条件,首先做辅助线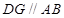 ,然后利用平行性得到相似比,
,然后利用平行性得到相似比,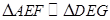 ,
,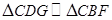 ,然后得到比例相等。充分利用比值问题转化得到结论。
,然后得到比例相等。充分利用比值问题转化得到结论。
证明:过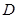 作
作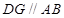 ,交
,交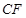 于
于 ,∴
,∴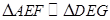 ,
,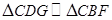 ,
,
∴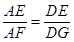 ,
,  , ∵
, ∵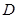 为
为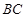 的中点,
的中点,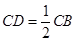 ,
,
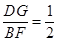 ,
,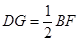 ,
,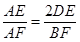 ,即
,即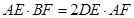 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com