题目列表(包括答案和解析)
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
，乙及格概率为
，丙及格概率为
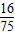
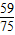
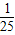
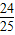
，则三人中至少有一人及格的概率为（ ）
，乙及格概率为
，丙及格概率为
，则三人中至少有一人及格的概率为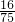
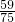
甲、乙、丙三位同学用计算机学习数学，每天上课后独立完成六道自我检测题，甲答及格的概率为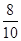
，乙答及格的概率为
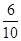，丙答及格的概率为
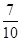，三人各答一次，则三人中只有一人答及格的概率为
A．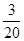
B．
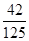C．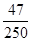
D．以上均不对
甲、乙、丙三位同学用计算机联网学习数学，每天上课后独立完成六道自我检测题，甲答及格的概率为
；乙答及格的概率为
；丙答及格的概率为
，三人各答一次，则三人中只有一人答及格的概率为（ ）
A．
B．
C．
D．以上全不对
一、选择题
1－5 D D B B D 6－10 D D C A B
二、填空题
11、
12、
13、
14、
=___5___；当ｎ＞４时，
＝
15。12种
三、解答题
16、（1）由条件
--------- (6′)
（2）z1+z2=(m2+3)+(m2-1)i--------- (8′)
|z1+z2|=
-----(10′)
=
,|z1+z2|min=
---------
(12′)
17、解：由
得
，所以
----------4分
故面积S＝
---------------------7分
＝
------------------10分
18、解：
----------------------3分
---------------- 7分
令
，得：
---------------10分
所以展开式中的常数项为：
。----------------------11分
19、解：（Ⅰ）由
的图象经过P（0，2），知d=2，所以
----------------------2分
由在
处的切线方程是
，知
---------------------6分
故所求的解析式是 
----------------------7分
（Ⅱ）
解得 
当
当
故
内是增函数，在
内是减函数，
在
内是增函数. ----------------------14分
20、解：（1）3个旅游团选择3条不同线路的概率为：P1=
-----------------3分
（2）恰有两条线路没有被选择的概率为：P2=
--------------6分
（3）设选择甲线路旅游团数为ξ，则ξ=0，1，2，3 -----------------7分
P（ξ=0）=
P（ξ=1）=
P（ξ=2）= 
P（ξ=3）= 
------------------11分
∴ξ的分布列为：
ξ
0
1
2
3
----------------------12分
∴期望Eξ=0×+1×+2×+3×=
---------------------14分
21、(1）当
时， 原等式变为
---2分
令
得 
---------------------5分
（2）因为
所以
----------------------7分
①当
时。左边=
，右边
左边=右边，等式成立。---------------------8分
②假设当
时，等式成立，即
-------9分
那么，当
时，
左边
右边。-------------1`2分
故当时，等式成立。
综上①②，当
时，
-------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com