
题目列表(包括答案和解析)
(本小题满分16分)定义在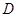 上的函数
上的函数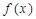 ,如果满足:对任意
,如果满足:对任意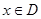 ,存在常数
,存在常数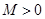 ,都有
,都有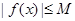 成立,则称
成立,则称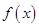 是
是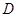 上的有界函数,其中
上的有界函数,其中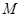 称为函数
称为函数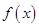 的上界.
的上界.
已知函数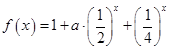 ;
;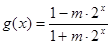 .
.
(1)当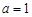 时,求函数
时,求函数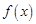 在
在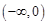 上的值域,并判断函数
上的值域,并判断函数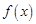 在
在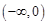 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数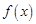 在
在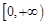 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数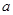 的取值范围;
的取值范围;
(3)若 ,函数
,函数 在
在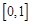 上的上界是
上的上界是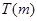 ,求
,求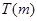 的取值范围.
的取值范围.
.(本小题满分16分)
已知函数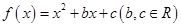 ,并设
,并设 ,
,
(1)若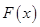 图像在
图像在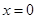 处的切线方程为
处的切线方程为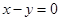 ,求
,求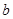 、
、 的值;
的值;
(2)若函数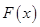 是
是 上单调递减,则
上单调递减,则
① 当 时,试判断
时,试判断 与
与 的大小关系,并证明之;
的大小关系,并证明之;
② 对满足题设条件的任意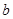 、
、 ,不等式
,不等式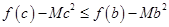 恒成立,求
恒成立,求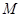 的取值范围
的取值范围
(本小题满分16分)
已知等差数列 中,
中,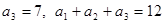 ,令
,令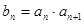 ,数列
,数列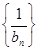 的前
的前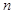 项和为
项和为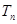 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证: ;
;
(3)是否存在正整数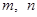 ,且
,且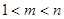 ,使得
,使得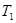 ,
, ,
,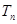 成等比数列?若存在,求出
成等比数列?若存在,求出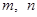 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分16分)已知椭圆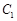 :
: 的离心率为
的离心率为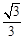 ,直线
,直线
 :
: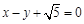 与椭圆
与椭圆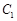 相切.
相切.
(1)求椭圆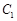 的方程;
的方程;
(2)设椭圆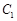 的左焦点为
的左焦点为 ,右焦点为
,右焦点为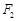 ,直线
,直线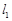 过点
过点 且垂直与椭圆的长轴,动直线
且垂直与椭圆的长轴,动直线 垂直于直线
垂直于直线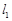 于点
于点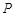 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点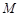 ,求点
,求点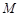 的轨迹
的轨迹 的方程.
的方程.
(本小题满分16分)
已知数列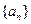 满足
满足 ,(1)若
,(1)若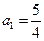 ,求
,求 ;
;
(2)是否存在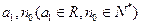 ,使当
,使当 时,
时, 恒为常数。若存在求
恒为常数。若存在求 ,否则说明理由;
,否则说明理由;
(3)若 ,求
,求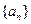 的前
的前 项的和
项的和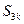 (用
(用 表示)
表示)
1、1
2、10
3、-49
4、70
5、
6、27 7、直角三角形 8、70 9、3 10、2
11、6 12、3<x<2 13、3
13、3 14、
14、
15解:(1) ………3分
………3分


 =28-3n
………7分
=28-3n
………7分
(2)


 ………10分
………10分

 =
= ………14分
………14分
16解:(1)由题意得 ……………………3分
……………………3分
由②得 或
或 ,代入①③检验得
,代入①③检验得 . ……………………5分
. ……………………5分
(2)由题意得 , ……………………7分
, ……………………7分
解得 或
或 ,检验得
,检验得 ,m=-1 ……………………10分
,m=-1 ……………………10分
(3)由题意得 ……………………12分
……………………12分
解得
所以 或
或 ……………………15分
……………………15分
17解、(I)由题意及正弦定理,得 ①,
①,
 ②, ……………………4分
②, ……………………4分
两式相减,得 .
………………………6分
.
………………………6分
(II)由 的面积
的面积 ,得
,得 , …………8分
, …………8分
由余弦定理,得 …………………10分
…………………10分
 ………………12分
………………12分
又 所以
所以 .
……………14分
.
……………14分
18 解:(1)A、B、C三点共线知存在实数 ………3分
………3分
即 ,
,
则 ………7分
………7分
(2) ………9分
………9分
 ………13分
………13分
当 ………15分
………15分
19解:(I)m•n= ┉┉┉┉2分
┉┉┉┉2分
= =
= ┉┉┉┉┉4分
┉┉┉┉┉4分
∵m•n=1∴ ┉┉┉┉┉┉5分
┉┉┉┉┉┉5分
 =
= ┉┉┉┉┉┉7分
┉┉┉┉┉┉7分
(2)∵(
由正弦定理得 ┉┉┉┉┉┉9分
┉┉┉┉┉┉9分
∴
∴
∵
∴ ,且
,且
∴ ┉┉┉┉┉┉12分
┉┉┉┉┉┉12分
∴
∴ ┉┉┉┉┉┉14分
┉┉┉┉┉┉14分
又∵f(x)=m•n= ,
,
∴f(A)=
故函数f(A)的取值范围是(1, )
┉┉┉┉┉┉16分
)
┉┉┉┉┉┉16分
20.(1)由 …………………………………2分
…………………………………2分
 …………………5分
…………………5分
(2)q=1时,S=49
q≠1时,S=
=2 ………………9分
………………9分
(3)∵
∴
∴
当 ……………………………………11分
……………………………………11分
∴当


设T=
∴
= …………………………………………14分
…………………………………………14分
当51≤n≤100时,
=295+
=295
=295 …………………………………16分
…………………………………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com