
题目列表(包括答案和解析)
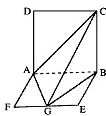 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=| 1 | 2 |
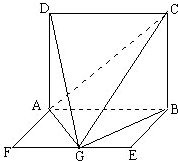 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,G是线段EF的中点,且B点在平面AGC内的射影在CG上.
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,G是线段EF的中点,且B点在平面AGC内的射影在CG上.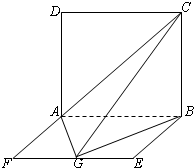 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=| 1 | 2 |
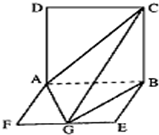 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=| 1 | 2 |
 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=| 1 | 2 |
一选择题
CDDAB BBCCC BB
二填空题
13、2000 14、2 15、 16、8+π
16、8+π
17解:(1)∵(x)=2sin (
( +x)×
+x)× cos2x-1=1-cos(
cos2x-1=1-cos( +2x)-
+2x)- cos2x-1
cos2x-1
=sin2x- cos2x=2sin(2x-
cos2x=2sin(2x- )…………………3分
)…………………3分
∴T=π……………………………………………………………4分
由2kπ- ≤2x-
≤2x- ≤2kπ得 kπ-
≤2kπ得 kπ- ≤x≤kπ+
≤x≤kπ+ π(k∈Z)
π(k∈Z)
即f(x)单调增区间为[kπ- ,kπ+
,kπ+ ](k∈Z)………………6分
](k∈Z)………………6分
(2)若p成立,即x∈[ ,
, ]时,2x-
]时,2x- ∈[
∈[ ,
, ],f(x)∈[1,2],……8分
],f(x)∈[1,2],……8分
由ㄏf(x)-mㄏ< 3=>m-3<f(x)<m+3………………………………… 9分
∵p是q的充分条件,
∴ m-3<1 m+3>2,解得-1<m<4,即m的取值范围是(-1,4)…………… 12分
18. 解:(Ⅰ)设事件 表示甲运动员射击一次,恰好击中9环以上(含9环),则
表示甲运动员射击一次,恰好击中9环以上(含9环),则
 .
……………….3分
.
……………….3分
甲运动员射击3次均未击中9环以上的概率为
 .
…………………5分
.
…………………5分
所以甲运动员射击3次,至少有1次击中9环以上的概率为
 .
………………6分
.
………………6分
(Ⅱ)记乙运动员射击1次,击中9环以上为事件 ,则
,则
 …………………8分
…………………8分
由已知 的可能取值是0,1,2.
…………………9分
的可能取值是0,1,2.
…………………9分
 ;
;
 ;
;
 .
.
 的分布列为
的分布列为

0
1
2

0.05
0.35
0.6
………………………10分
所以
故所求数学期望为 .
………………………12分
.
………………………12分
19.解法一(几何法)
(1)证明:正方形ABCD ∵面ABCD⊥面ABEF且交于AB,
∵面ABCD⊥面ABEF且交于AB,
∴CB⊥面ABEF ∵AG,GB 面ABEF, ∴CB⊥AG,CB⊥BG
面ABEF, ∴CB⊥AG,CB⊥BG
又AD=2a,AF=a,ABEF是矩形,G是EF的中点,
∴AG=BG= ,AB=2a,AB2=AG2+BG2,∴AG⊥BG ∵CG∩BG=G,
,AB=2a,AB2=AG2+BG2,∴AG⊥BG ∵CG∩BG=G,
∴AG⊥平面CBG 面AG 面AGC, 故平面AGC⊥平面BGC.…4分
面AGC, 故平面AGC⊥平面BGC.…4分
 (2)解:如图,由(Ⅰ)知面AGC⊥面BGC,
(2)解:如图,由(Ⅰ)知面AGC⊥面BGC,
且交于GC,在平面BGC内作BH⊥GC,
垂足为H,则BH⊥平面AGC,
∴∠BGH是GB与平面AGC所成的角
∴Rt△CBG中
又BG= ,∴
,∴ ……8分
……8分
(3)由(Ⅱ)知,BH⊥面AGC, 作BO⊥AC,垂足为O,连结HO,
则HO⊥AC,∴∠BOH为二面角B―AC―G的平面角在Rt△ABC中,
在Rt△BOH中,
即二面角B―AC―G的平面角的正弦值为 .
……12分
.
……12分
[方法二](向量法)
解法:以A为原点,AF所在直线为x轴,AB所在直线为y轴,AD所在直线为z轴建立直角坐标系,
则A(0,0,0),B(0,2a,0),C(0,2a,2a),G(a,a,0),F(a,0,0)
(2)由题意可得 ,
,
 , 设平面AGC的法向量为
, 设平面AGC的法向量为 ,
,
由

(3)因 是平面AGC的法向量,又AF⊥平面ABCD,
是平面AGC的法向量,又AF⊥平面ABCD,
平面ABCD的法向量 , 得
, 得
∴二面角B―AC―G的的平面角的正弦值为 .
.
20. (Ⅰ)函数 的定义域为:
的定义域为: .
…………………………1分
.
…………………………1分
∵ , ∴
, ∴ .
.
令 ,则
,则 .
……………3分
.
……………3分
当 在
在 上变化时,
上变化时, 的变化情况如下表
的变化情况如下表





+
0
-

ㄊ
极大值
ㄋ
∴函数 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 . …………6分
. …………6分
(Ⅱ)由题意可知: ,
…………………7分
,
…………………7分
曲线 在点
在点 处的切线的斜率为
处的切线的斜率为 . …8分
. …8分
∴切线方程为: .
……………9分
.
……………9分
∴ .
.
∴ .
……………10分
.
……………10分
∵切线方程为 , ∴
, ∴ . ∴
. ∴ .
.
∴曲线 在点
在点 处的切线的斜率
处的切线的斜率 . ………12分
. ………12分
21. 解:(1)由题意设椭圆的标准方程为 ,
,
由已知得: ,
,
∴ ,
, ,∴
,∴
∴椭圆的标准方程为
(2)设 、
、 ,
,
联立 得
得

又 ,
,
因为以 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,
,
∴ ,即
,即 .
.
∴
∴
∴
解得:
 ,且均满足
,且均满足 .
.
当 时,
时, 得方程为
得方程为 ,直线过定点(2,0),与已知矛盾;
,直线过定点(2,0),与已知矛盾;
当 时,
时, 得方程为
得方程为 ,直线过定点(
,直线过定点( ,0),
,0),
所以直线 过定点,定点坐标为(
过定点,定点坐标为( ,0).
,0).
22(本小题满分12分)
设Sn是数列 的前n项和,且
的前n项和,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 使
使
 ,求
,求 的通项公式;
的通项公式;
(3)设 ,且数列
,且数列 的前n项和为Tn,试比较Tn与
的前n项和为Tn,试比较Tn与 的大小.
的大小.
解:(1)∵ ,∴
,∴ ,
,
于是an+1=Sn+1-Sn=(2 an+1-2)-(2 an-2),即an+1=2an. …………2分
又a1=S1=2 a1-2, 得a1=2. …………3分
∴ 是首项和公比都是2的等比数列,故an=2n.
…………4分
是首项和公比都是2的等比数列,故an=2n.
…………4分
(2) 由a1b1=(2×1-1)×21+1+2=6及a1=2得b1=3. …………5分
当 时,
时,
 ,
,
∴ .
…………7分
.
…………7分
∵an=2n,∴bn=2n+1( ).
…………8分
).
…………8分
∴ …………10分
…………10分
(3) . …………12分
. …………12分
 .
.
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com