.files/image176.jpg)
则C(0,0,0),C1(0,0,2),
A(1,0,0),B1(0,1,2),A1(1,0,2)
∵M为A1B1中点,
.files/image178.gif) …………………………4分
…………………………4分
(1).files/image180.gif)
.files/image182.gif) ……………………6分
……………………6分
.files/image184.gif) ∥面AC1M,又∵B1C
∥面AC1M,又∵B1C.files/image186.gif) 面AC1M,
面AC1M,
∴B1C∥面AC1M.…………………………8分
(2)设平面AC1M的一个法向量为.files/image188.gif)
.files/image190.gif)
.files/image192.gif)
.files/image194.gif) …………………………………………………………10分
…………………………………………………………10分
.files/image196.gif)
则.files/image198.gif) …………………………12分
…………………………12分
20.解:(1).files/image200.gif) ………………2分
………………2分
.files/image202.gif) 的等差中项,
的等差中项,
.files/image204.gif)
解得q=2或.files/image206.gif) (舍去),………………………………………………4分
(舍去),………………………………………………4分
.files/image208.gif) ………………5分
………………5分
(2)由(1)得.files/image210.gif) ,
,
当n=1时,A1=2,B1=(1+1)2=4,A1<B1;
当n=2时,A2=6,B2=(2+1)2=9,A2<B2;
当n=3时,A3=14,B3=(3+1)2=16,A3<B3;
当n=4时,A4=30,B4=(4+1)2=25,A4>B4;
由上可猜想,当1≤n≤3时,An<Bn;当n≥4时,An>Bn.……………………8分
下面用数学归纳法给出证明:
①当n=4时,已验证不等式成立.
②假设n=k(k≥4)时,Ak>Bk.成立,即.files/image212.gif) ,
,
.files/image214.gif)
即当n=k+1时不等式也成立,
由①②知,当.files/image216.gif)
综上,当.files/image218.gif) 时,An<Bn;当
时,An<Bn;当.files/image220.gif)
21.解:(1)设.files/image222.gif) .
.
由题意得.files/image224.gif) ……………………2分
……………………2分
∵m>1,∴轨迹C是中心在坐标原点,焦点在x轴上的椭圆(除去x轴上的两项点),其
中长轴长为2.files/image226.gif) ,短轴长为2.………………………………………………4分
,短轴长为2.………………………………………………4分
(2)当m=.files/image228.gif) 时,曲线C的方程为
时,曲线C的方程为.files/image230.gif)
由.files/image232.gif) ………………6分
………………6分
令.files/image234.gif)
此时直线l与曲线C有且只有一个公共点.………………………………8分
(3)直线l方程为2x-y+3=0.
设点.files/image236.gif) 表示P到点(1,0)的距离,d2表示P到直线x=2的距离,
表示P到点(1,0)的距离,d2表示P到直线x=2的距离,
则.files/image238.gif)
.files/image240.gif) …………………………10分
…………………………10分
令.files/image242.gif)
则.files/image244.gif)
令.files/image246.gif) ……………………………………………………12分
……………………………………………………12分
.files/image248.gif)
.files/image250.gif)
.files/image252.gif)
∴.files/image254.gif) 的最小值等于椭圆的离心率.……………………………………14分
的最小值等于椭圆的离心率.……………………………………14分
22.(1)由已知.files/image256.gif)
.files/image258.gif) ,
,
.files/image260.gif)
.files/image262.gif) …………………………………………………………2分
…………………………………………………………2分
又当a=8时,.files/image264.gif)
.files/image266.gif)
.files/image268.gif) 上单调递减.……………………………………………………4分
上单调递减.……………………………………………………4分
(2).files/image270.gif)
.files/image272.gif)
.files/image274.gif) ……………………6分
……………………6分
.files/image276.gif)
.files/image278.gif)
.files/image280.gif)
.files/image282.gif)
.files/image284.gif) ………………………………………………8分
………………………………………………8分
(3)设.files/image286.gif)
且.files/image288.gif)
由(1)知.files/image290.gif)
.files/image292.gif)
∴△ABC为钝角三角形,且∠B为钝角.…………………………………………11分
若△ABC为等腰三角形,则|AB|=|BC|,
.files/image294.gif)
.files/image296.gif)
此与(2)矛盾,
∴△ABC不可能为等腰三角形.………………………………………………14分

 .
. ),f(
),f( )是否成等比数列,并证明f(
)是否成等比数列,并证明f( )≤f(
)≤f( );
); 为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.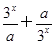 是R上的偶函数.
是R上的偶函数.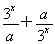 是R上的偶函数.
是R上的偶函数.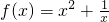 在(1,+∞)上的单调性,并用定义法加以证明;
在(1,+∞)上的单调性,并用定义法加以证明;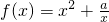 在区间(1,+∞)上的单调递增,求实数a的取值范围.
在区间(1,+∞)上的单调递增,求实数a的取值范围.