练习册

  • 练习册
  • 试题
    A. B. C. D. 饶平县第一中学2009年普通高考测试题(一)数 学第二部分注意事项:第Ⅱ卷全部是非选择题.必须在答题卡非选择题答题区域内.用黑色字迹钢笔或签字笔作答.不能答在试卷上.否则答案无效. 【查看更多】

     

    题目列表(包括答案和解析)

    某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人）另外750名工人参加过长期培训（称为B类工人）．现用分层抽样的方法（按A类、B类分两层）从该工厂的工人中抽取100名工人，调查他们的生产能力（此处生产能力指一天加工的零件数）．从A类工人中的抽查结果和从B类工人中的抽查结果如下表1和表2．
    表1
    生产能力分组 [110，120） [120，130） [130，140） [140，150）
    人数 8 x 3 2
    表2
    生产能力分组 [110，120） [120，130） [130，140） [140，150）
    人数 6 y 27 18
    （Ⅰ）先确定x、y的值，再补齐下列频率分布直方图．

    （Ⅱ）完成下面2×2列联表，并回答能否有99.9%的把握认为“工人的生产能力与工人的类别有关”？
    生产能力分组 [110，130） [130，150） 合计
    A类工人
    B类工人
    合计
    附：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)

    P（K2≥k） 0，05 0.025 0.01 0.005
    k 3.841 5.024 6.635 7.879

    查看答案和解析>>

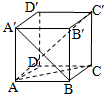    如图，在正方体ABCD-A′B′C′D′中，直线A′B和直线AC、CC′、C′A所成的角的大小分别是α、β、γ，则α、β、γ的大小关系是（　　）

    查看答案和解析>>

    （2012•武昌区模拟）通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如下的列联表：
    男 女 总计
    走天桥 40 20 60
    走斑马线 20 30 50
    总计 60 50 110
    由K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，算得K2=
    110×(40×30-20×20)2
    60×50×60×50
    ≈7.8
    参照独立性检验附表，得到的正确结论是（　　）

    查看答案和解析>>

    设向量
    a
    =（1，cos2θ），
    b
    =（2，1），
    c
    =（4sinθ，1），
    d
    =（
    1
    2
    sinθ，1）．
    （1）若θ∈（0，
    π
    4
    ），求
    a
    •
    b
    -
    c
    •
    d
    的取值范围；
    （2）若θ∈[0，π），函数f（x）=|x-1|，比较f（
    a
    •
    b
    ）与f（
    c
    •
    d
    ）的大小．

    查看答案和解析>>

    “中国式过马路”存在很大的交通安全隐患．某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如下列联表：
    男性 女性 合计
    反感 10
    不反感 8
    合计 30
    已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
    8
    15
    ．
    （Ⅰ）请将上面的列表补充完整（在答题卡上直接填写结果，不需要写求解过程），并据此资料分析反感“中国式过马路”与性别是否有关？（x2=
    (a+b+c+d)(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，当Χ2＜2.706时，没有充分的证据判定变量性别有关，当Χ2＞2.706时，有90%的把握判定变量性别有关，当Χ2＞3.841时，有95%的把握判定变量性别有关，当Χ2＞6.635时，有99%的把握判定变量性别有关）
    （Ⅱ）若从这30人中的女性路人中随机抽取2人参加一活动，记反感“中国式过马路”的人数为X，求X的分布列和数学期望．

    查看答案和解析>>

    一、选择题（本大题共8小题，每小题5分，共40分）

    1.B   2. C  3. D    4.C   5.B   6.D   7.A   8. B.

     

    二、填空题（本大题共6小题，每小题5分，共30分）

    9.； 10.（-1，2）； 11.0；  12.（或）；

    13.（1） 或 ；（2）16；（3）.

    三、解答题（本大题共6小题，共80分）

    14.（本小题满分12分）

    解：（Ⅰ）∵

    当时，其图象如右图所示.---4分

    （Ⅱ）函数的最小正周期是，其单调递增区间是；由图象可以看出，当时，该函数的最大值是.--------------7分

    （Ⅲ）若x是△ABC的一个内角，则有，∴

    由，得

    ∴  ∴ ，，故△ABC为直角三角形. --------------12分

    15．（本小题满分12分）

    解：（Ⅰ）

           --------6分

    （Ⅱ）当时，

     ----------12分

     

    16．（本小题满分14分）

    解：（Ⅰ）该几何体的直观图如图1所示，它是有一条

    侧棱垂直于底面的四棱锥. 其中底面ABCD是边长为6的

    正方形，高为CC1=6，故所求体积是

           ------------------------4分

     （Ⅱ）依题意，正方体的体积是原四棱锥体积的3倍，

    故用3个这样的四棱锥可以拼成一个棱长为6的正方体，

    其拼法如图2所示. ------------------------6分

       证明:∵面ABCD、面ABB1A1、面AA1D1D为全等的

    正方形，于是

      故所拼图形成立.---8分

    （Ⅲ）方法一：设B1E，BC的延长线交于点G，

     连结GA，在底面ABC内作BH⊥AG，垂足为H，

    连结HB1，则B1H⊥AG，故∠B1HB为平面AB1E与

    平面ABC所成二面角或其补角的平面角. --------10分

      在Rt△ABG中，，则

    ，，

    ，故平面AB1E与平面ABC所成二面角的余弦值为.---14分

       方法二：以C为原点，CD、CB、CC1所在直线分别为x、y、z轴建立直角坐标系（如图3），∵正方体棱长为6，则E（0，0，3），B1（0，6，6），A（6，6，0）.

     设向量n=（x，y，z），满足n⊥，n⊥，

    于是，解得.       --------------------12分

      取z=2，得n=（2，-1，2）. 又（0，0，6），

    故平面AB1E与平面ABC所成二面角的余弦值为. ----------------14分

     

    17．（本小题满分14分）

    解：分别记该考生考上第1、2、3批分数线为事件A、B、C，被相应志愿录取为事件Ai、Bi、Ci，（i=a、b）, 则以上各事件相互独立.  -------------------------------------2分

    （Ⅰ）“该考生被第2批b志愿录取”包括上第1批分数线和仅上第2批分数线两种情况，故所求概率为

         

    .  -----------------------------------------------------------------------------------6分

    （Ⅱ）设该考生所报志愿均未录取的概率为，则

               

              

             .

         ∴该考生能被录取的概率为. ------------10分

    表 二

    批次

    a

    b

    第2批

    0.9

    0.05

    第3批

    0.048

    0.0020

    从表中可以看出，该考生被第2批a志愿录取的概率最大，故最有可能在第2批a志愿被录取. ------14分

     

    18．（本小题满分14分）

    解：（Ⅰ）∵，当时，.

         ∴在[1，3]上是增函数.---------------------------------3分

         ∴当时，≤≤，即 -2≤≤26.

          ∴存在常数M=26，使得，都有≤M成立.

           故函数是[1，3]上的有界函数.---------------------------6分

    （Ⅱ）∵. 由≤1，得≤1

       ∴ 

           令，则.

          当时，有，

    ∴在[0，+∞上单调递减.   -------------------------------10分

    故当t=0 时，有；

    又，当t→+∞时，→0，

    ∴ ，从而有≤0，且.  ∴0≤a≤1；                               故所求a的取值范围为0≤a≤1.---------------------------------------------14分

     

    19．（本小题满分14分）

    解：（Ⅰ）易知，椭圆的半焦距为：，

     又抛物线的准线为：.

    设双曲线M的方程为，依题意有，

    故，又.

    ∴双曲线M的方程为. ------------------------4分

    （Ⅱ）设直线与双曲线M的交点为、两点

    联立方程组 消去y得  ，

    ∵、两点的横坐标是上述方程的两个不同实根， ∴

    ∴，从而有

    ，.

    又，

    ∴.

    ① 若，则有 ，即 .

    ∴当时，使得. -----------------------------8分

    ② 若存在实数,使A、B两点关于直线对称，则必有 ，

    因此，当m=0时，不存在满足条件的k；------------------------------------10分

    当时，由 得

      

    ∵A、B中点在直线上，

    ∴ 代入上式得

    ；又， ∴

    将代入并注意到，得 .

    ∴当时，存在实数，使A、B两点关于直线对称.--14分

    如上各题若有其它解法，请评卷老师酌情给分.

     

     

     

     


    同步练习册答案