练习册

  • 练习册
  • 试题
    -2, (C), (D)1或. 【查看更多】

     

    题目列表(包括答案和解析)

    （08年新建二中模拟文） (12分)    已知是定义在R上的函数，其图象交x轴于A、B、C三点．若点B的坐标为 (2，0)，且f (x) 在[－1，0]和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性．
    　　(1)求c的值；
    　　(2)在函数f (x)的图象上是否存在一点M(x0，y0)，使得f (x)在点M的切线斜率为3b？若存在，求出点M的坐标；若不存在，请说明理由；
    　　(3)求| AC |的取值范围．

    查看答案和解析>>

    （18）

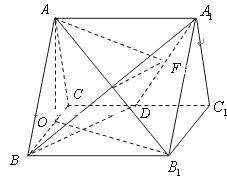
    如图，正三棱柱ABC－A1B1C1的所有棱长都为2，D为CC1中点。

    （1）求证：AB1⊥面A1BD；

    （2）求二面角A－A1D－B的大小；

    （3）求点C到平面A1BD的距离。

    查看答案和解析>>

    （20）

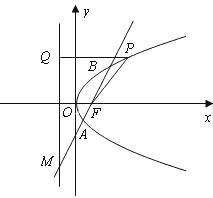
    如图，已知点F（1，0），直线l：x＝－1，P为平面上的动点，过P作直线l的垂线，垂足为点Q，且。

    （1）求动点P的轨迹C的方程；

    （2）过点F的直线交轨迹C于A、B两点，交直线l于点M，已知，，求的值。

    查看答案和解析>>

    （12分）A、B、C为△ABC的三内角，且其对边分别为a、b、c．若＝(－cos，sin)，＝(cos，sin)，且·＝．

    　 （1）求A；

    　 （2）若a＝2，三角形面积S＝，求b+c的值．

    查看答案和解析>>

     （12′）设A={x|x2－ax+a2－19=0},B={x|x2－5x+6=0},C={x|x2+2x－8=0}

       （1）A∩B=A∪B,求a的值；

       （2）ФA∩B ,且A∩C=Ф，求a的值（注：应为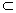≠的上下合成）；

       （3） A∩B=A∩C≠Ф，求a的值.

     

     

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    一、选择题

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    B

    B

    A

    B

    D

    B

    C

    C

    A

    B

    C

    A

    C

    D

    C

     

    二、填空题

    16.；17.；18等边三角形；19.3；20.①②④

    三、解答题

    21解（I）由题意及正弦定理，得  ①，

      ②，………………1分

    两式相减，得．　　…………………2分

    （II）由的面积，得，……4分

    由余弦定理，得                         　　　……………5分

    所以．　…………6分

    22 .解：（Ⅰ）      ……2分

    （Ⅱ）   

    ∴数列从第10项开始小于0                ……4分

    （Ⅲ）

    23解：（Ⅰ）由得

    即：

    ∴…………2分

    而又

    而…………4分

    （Ⅱ）利用余弦定理可解得： 

          ，∵，故有或…………7分

    24解:（I）设等比数列{an}的公比为q, 则q≠0, a2= = , a4=a3q=2q

    　　所以 + 2q= ,     解得q1= , q2= 3,            …………1分

    　　当q1=, a1=18.所以 an=18×（ ）n－1= = 2×33－n.

    　　当q=3时, a1= ,所以an=×=2×3n－5.         …………3分

    （II）由（I）及数列公比大于，得q=3，an=2×3n－5 ，…………4分

         ，

    （常数），   ．

    所以数列为首项为－4，公差为1的等差数列，……6分　　

    ．     …………7分

    25.解:(Ⅰ)  n=1时      ∴

    n=2时         ∴

    n=3时     ∴       …………2分

    (Ⅱ)∵   ∴

    两式相减得:   即

    也即

    ∵    ∴  即是首项为2,公差为4的等差数列

    ∴          …………5分

    (Ⅲ)

    ∴

       …………7分

    ∵对所有都成立   ∴  即

    故m的最小值是10       …………8分

     

     


    同步练习册答案