
题目列表(包括答案和解析)
(本题满分12分)已知![]() 是定义域为[-3,3]的函数,并且设
是定义域为[-3,3]的函数,并且设![]() ,
,![]() ,其中常数c为实数.(1)求
,其中常数c为实数.(1)求![]() 和
和![]() 的定义域;(2)如果
的定义域;(2)如果![]() 和
和![]() 两个函数的定义域的交集为非空集合,求c的取值范围;(3)当
两个函数的定义域的交集为非空集合,求c的取值范围;(3)当![]() 在其定义域内是奇函数,又是增函数时,求使
在其定义域内是奇函数,又是增函数时,求使![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
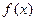 是定义域为[-3,3]的函数,并且设
是定义域为[-3,3]的函数,并且设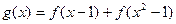 ,
,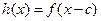 ,其中常数c为实数.(1)求
,其中常数c为实数.(1)求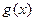 和
和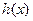 的定义域;(2)如果
的定义域;(2)如果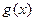 和
和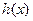 两个函数的定义域的交集为非空集合,求c的取值范围;(3)当
两个函数的定义域的交集为非空集合,求c的取值范围;(3)当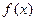 在其定义域内是奇函数,又是增函数时,求使
在其定义域内是奇函数,又是增函数时,求使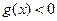 的自变量
的自变量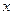 的取值范围.
的取值范围.已知奇函数f(x)的定义域为R,且f(x)在[0,+∞)上是增函数,是否存在实数m,使f(cos2θ-3)+f(4m-2mcosθ)>f(0)对所有θ∈[0,![]() ]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由.
]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由.
已知奇函数f(x)的定义域为R,且f(x)在[0,+∞)上是增函数,是否存在实数m,使f(cos2θ-3)+f(4m-2mcosθ)>f(0)对所有θ∈[0,![]() ]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
已知函数f(x)=lg(ax-kbx )(k是正实数,a>1>b>0)的定义域为(0,+∞),问是否存在实数a,b,当x∈(1,+∞)时,f(x)的值取到一切正实数,且f(3)=lg4;如果存在,求出a,b的值;如果不存在,请说明理由。
一、选择题(本大题共12小题,每小题5分,共60分)
1~5 D A B D C 6~
二、填空题(本大题共4小题,每小题4分,共16分)
13..files/image202.gif) ; 14.21 ;
15.
; 14.21 ;
15..files/image018.gif) ; 16.
; 16..files/image205.gif) .
.
三、解答题(本大题共6小题,共74分)
17.(本题满分13分)
解:(1)甲、乙两卫星各自预报一次,记“甲预报准确”为事件A,“乙预报准确”为事件B.则两卫星只有一颗卫星预报准确的概率为:
.files/image207.gif) … 4分
… 4分
= 0.8×(1 - 0.75) + (1 - 08)×0.75 = 0.35 …………6分
答:甲、乙两卫星中只有一颗卫星预报准确的概率为0.35 ………7分
(2) 甲独立预报3次,至少有2次预报准确的概率为
.files/image209.gif) …………10分
…………10分
=.files/image211.gif) =0.896
………………………12分
=0.896
………………………12分
答:甲独立预报3次,至少有2次预报准确的概率为0.896. ……… 13分
18.(本题满分13分)
解:(1)∵.files/image213.gif) …………………2分
…………………2分
=.files/image215.gif) =
=.files/image217.gif) ……………6分
……………6分
∴函数.files/image144.gif) 的最小正周期
的最小正周期.files/image219.gif) …………………7分
…………………7分
又由.files/image221.gif) 可得:
可得:
.files/image144.gif) 的单调递增区间形如:
的单调递增区间形如:.files/image223.gif) ……9分
……9分
(2) ∵.files/image225.gif) 时,
时,.files/image227.gif) ,
,
∴.files/image229.gif) 的取值范围是
的取值范围是.files/image231.gif) ………………11分
………………11分
∴函数.files/image144.gif) 的最大值是3,最小值是0
的最大值是3,最小值是0
从而函数.files/image144.gif) 的是
的是.files/image233.gif) …………13分
…………13分
19.(本题满分12分)
解:(1) ∵.files/image235.gif) ∴由已知条件可得:
∴由已知条件可得:.files/image237.gif) ,并且
,并且.files/image239.gif) ,
,
解之得:.files/image241.gif) ,
,.files/image243.gif) ……………3分
……………3分
从而其首项.files/image245.gif) 和公比
和公比.files/image247.gif) 满足:
满足:.files/image249.gif)
.files/image251.gif)
.files/image253.gif) ………5分
………5分
故数列.files/image148.gif) 的通项公式为:
的通项公式为:.files/image255.gif) ……6分
……6分
(2) ∵.files/image257.gif)
数列.files/image259.gif) 是等差数列,
…………………………8分
是等差数列,
…………………………8分
∴.files/image261.gif)
=.files/image263.gif)
=.files/image265.gif) =
=.files/image267.gif) …………………10分
…………………10分
由于.files/image269.gif) ,当且仅当
,当且仅当.files/image271.gif) 最大时,
最大时,.files/image158.gif) 最大.
最大.
所以当.files/image158.gif) 最大时,
最大时,.files/image274.gif) 或6 …………………………12分
或6 …………………………12分
20.(本题满分12分)
解:(1) ∵.files/image162.gif) 为奇函数 ∴
为奇函数 ∴.files/image276.gif) ………2分
………2分
∵.files/image278.gif) ,导函数
,导函数.files/image164.gif) 的最小值为-12 ∴
的最小值为-12 ∴.files/image280.gif) ……3分
……3分
又∵直线.files/image170.gif) 的斜率为
的斜率为.files/image283.gif) ,
,
并且.files/image166.gif) 的图象在点P
的图象在点P.files/image168.gif) 处的切线与它垂直
处的切线与它垂直
∴.files/image285.gif) ,即
,即.files/image287.gif) ∴
∴.files/image289.gif) ……………6分
……………6分
(2) 由第(1)小题结果可得:.files/image291.gif)
.files/image293.gif) ……………9分
……………9分
令.files/image295.gif) ,得
,得.files/image297.gif) ……………10分
……………10分
∵.files/image299.gif) ,
,.files/image301.gif) ,
,.files/image303.gif)
∴.files/image144.gif) 在
在.files/image173.gif) [-1, 3]的最大值为11,最小值为-16. ………12分
[-1, 3]的最大值为11,最小值为-16. ………12分
21.(本题满分12分)
解:(1) ∵函数.files/image180.gif) 有意义的充要条件为
有意义的充要条件为
.files/image305.gif) ,即是
,即是 .files/image307.gif)
.files/image251.gif)
.files/image310.gif)
∴函数.files/image180.gif) 的定义域为
的定义域为.files/image312.gif) …………3分
…………3分
∵函数.files/image182.gif) 有意义的充要条件为:
有意义的充要条件为:.files/image314.gif)
∴函数.files/image182.gif) 的定义域为
的定义域为.files/image316.gif) …………5分
…………5分
(2)∵由题目条件知.files/image312.gif)
.files/image318.gif)
.files/image320.gif)
∴.files/image322.gif) ,
…………………7分
,
…………………7分
∴c的取值范围是:[-5, 5] …………………8分
(3) .files/image324.gif) 即是
即是.files/image326.gif)
∵.files/image144.gif) 是奇函数,∴
是奇函数,∴.files/image328.gif) ………………9分
………………9分
又∵函数.files/image144.gif) 的定义域为
的定义域为.files/image330.gif) ,并且是增函数
,并且是增函数
∴ .files/image332.gif)
.files/image334.gif)
.files/image336.gif) ………………11分
………………11分
解之得.files/image186.gif) 的取值范围是:
的取值范围是:.files/image338.gif) =
=.files/image340.gif) …………12分
…………12分
22.(本题满分12分)
解:(1) 设双曲线的渐近线方程为.files/image342.gif) ,即
,即.files/image344.gif) ,
,
∵双曲线的渐近线与已知的圆相切,圆心到渐近线的距离等于半径
∴.files/image346.gif)
.files/image251.gif)
.files/image348.gif)
.files/image251.gif)
.files/image350.gif)
∴双曲线的渐近线的方程为:.files/image352.gif) ……………2分
……………2分
又设双曲线的方程为:.files/image354.gif) ,则
,则
∵双曲线的渐近线的方程为.files/image352.gif) ,且有一个焦点为
,且有一个焦点为.files/image356.gif)
∴.files/image358.gif)
.files/image360.gif) ,
………………4分
,
………………4分
解之得:.files/image362.gif) ,故双曲线的方程是:
,故双曲线的方程是:.files/image364.gif) ……………5分
……………5分
(2) 联立方程组.files/image366.gif) ,消去
,消去.files/image198.gif) 得:
得:.files/image369.gif) (*)…………6分
(*)…………6分
∵直线与双曲线C的左支交于两点,方程(*)两根.files/image371.gif) 、
、.files/image373.gif) 为负数,
为负数,
∴.files/image375.gif)
.files/image377.gif)
.files/image379.gif)
.files/image377.gif)
.files/image381.gif) …………8分
…………8分
又∵线段PQ的中点.files/image383.gif) 坐标满足
坐标满足
.files/image385.gif) ,
,.files/image387.gif) ……9分
……9分
∴直线.files/image194.gif) 的方程为:
的方程为:.files/image389.gif) ,
,
即是.files/image391.gif) ,
,.files/image393.gif)
直线.files/image194.gif) 在
在.files/image198.gif) 轴的截距
轴的截距.files/image395.gif) ……………………11分
……………………11分
又∵.files/image381.gif) 时,
时,.files/image397.gif) 的取值范围是:
的取值范围是:.files/image399.gif)
∴直线.files/image194.gif) 的截距
的截距.files/image200.gif) 的取值范围是
的取值范围是.files/image401.gif) ……12分
……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com