C．（选修模块 3 一 5 ）  
（ l ）在光电效应实验中，小明同学用同一实验装置（如图 l ）在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线，如图（ 2 ）所示．则
（ A ）乙光的频率小于甲光的频率 （ B ）甲光的波长大于丙光的波长 （ C ）丙光的光子能量小于甲光的光子能量 （ D ）乙光对应的光电子最大初动能小于丙光的光电子最大初动能
（ 2 ）用光照射某金属，使它发生光电效应现象，若增加该入射光的强度，则单位时间内从铝板表面逸出的光电子数

 

，从表面逸出的光电子的最大动量大小

 

（选填“增加”、“减小”或“不变，'）
（ 3 ）用加速后动能为Ek0的质子：

1 1

H轰击静止的原子核 x，生成两个动能均为Ek的

4 2

He核，并释放出一个频率为 v 的γ光子．写出上述核反应方程并计算核反应中的质量亏损．（光在真空中传播速度为 c ）

查看答案和解析>>

C． （选修3-5试题） 
（1）下列说法正确的是

 

A．原子核内部某个中子转变为质子和电子，产生的电子从原子核中发射出来，这就是β衰变
B．比结合能小的原子核结合成或分解成比结合能大的原子核时一定吸收核能
C．根据玻尔理论可知，氢原子辐射出一个光子后，氢原子的电势能增大，核外电子的运动速度减小．
D．德布罗意在爱因斯坦光子说的基础上提出物质波的概念，认为一切物体都具有波粒二象性．
（2）现用如图1下列几种能量的光子的光照射处于基态的氢原子，A：10.25eV、B：12.09eV、C：12.45eV，则能被氢原子吸收的光子是

 

（填序号），氢原子吸收该光子后可能产生

 

种频率的光子．氢原子能级图为：

（3）如图2（a）所示，在水平光滑轨道上停着甲、乙两辆实验小车，甲车系一穿过打点计时器的纸带，当甲车受到水平向右的瞬时冲量时，随即启动打点计时器，甲车运动一段距离后，与静止的乙车发生正碰并粘在一起运动，纸带记录下碰撞前甲车和碰撞后两车运动情况如图2（b）所示，电源频率为50Hz，求：甲、乙两车的质量比m_甲：m_乙．

查看答案和解析>>

D．为了测量一个量程为3V的电压表的内阻R_V（约几千欧），可以采用如图甲电路．

（1）试将如图乙所给实验仪器按实验电路连成测量电路．
（2）在测量时，可供选择的实验步骤有：
A．闭合开关K；
B．将电阻箱R₀的阻值调到最大；
C．将电阻箱R₀的阻值调到零；
D．调节电阻箱R₀的阻值使电压表的指针指示1.5V，记下此时R₀的值；
E．调节变阻器R的滑动片P，使电压表的指针指示3.0V；
F．把变阻器R的滑动片P滑到a端；
G．把变阻器R的滑动片P滑到b端；
H．断开开关K；
把必要的合理步骤选出来，按操作顺序将字母代号填在下面横线上

 

．
（3）若在步骤D中读出R₀的阻值为如图丙所示位置，则电压表的电阻为

 

Ω．用这种方法测出的电压表内阻与真实值相比偏

 

（填大或小）．

查看答案和解析>>

C．（选修模块 3 一 5 ）  
（ l ）在光电效应实验中，小明同学用同一实验装置（如图 l ）在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线，如图（ 2 ）所示．则
（ A ）乙光的频率小于甲光的频率 （ B ）甲光的波长大于丙光的波长 （ C ）丙光的光子能量小于甲光的光子能量 （ D ）乙光对应的光电子最大初动能小于丙光的光电子最大初动能
（ 2 ）用光照射某金属，使它发生光电效应现象，若增加该入射光的强度，则单位时间内从铝板表面逸出的光电子数______，从表面逸出的光电子的最大动量大小______（选填“增加”、“减小”或“不变，'）
（ 3 ）用加速后动能为Ek0的质子：

11

H轰击静止的原子核 x，生成两个动能均为Ek的

42

He核，并释放出一个频率为 v 的γ光子．写出上述核反应方程并计算核反应中的质量亏损．（光在真空中传播速度为 c ）

查看答案和解析>>

C． （选修3-5试题） 
（1）下列说法正确的是______
A．原子核内部某个中子转变为质子和电子，产生的电子从原子核中发射出来，这就是β衰变
B．比结合能小的原子核结合成或分解成比结合能大的原子核时一定吸收核能
C．根据玻尔理论可知，氢原子辐射出一个光子后，氢原子的电势能增大，核外电子的运动速度减小．
D．德布罗意在爱因斯坦光子说的基础上提出物质波的概念，认为一切物体都具有波粒二象性．
（2）现用如图1下列几种能量的光子的光照射处于基态的氢原子，A：10.25eV、B：12.09eV、C：12.45eV，则能被氢原子吸收的光子是______（填序号），氢原子吸收该光子后可能产生______种频率的光子．氢原子能级图为：

（3）如图2（a）所示，在水平光滑轨道上停着甲、乙两辆实验小车，甲车系一穿过打点计时器的纸带，当甲车受到水平向右的瞬时冲量时，随即启动打点计时器，甲车运动一段距离后，与静止的乙车发生正碰并粘在一起运动，纸带记录下碰撞前甲车和碰撞后两车运动情况如图2（b）所示，电源频率为50Hz，求：甲、乙两车的质量比m_甲：m_乙．

查看答案和解析>>

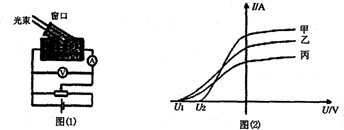
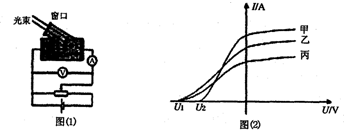
1．C由电荷数守恒和质量数守恒可知A、B错，由于镍63放出电子，故带正电，电势比铜片电势高，C正确，电流方向从铜片到镍，D错

2．C

3．A由可知，A正确

4．B将分子粗略地看成一个小立体，则个

5．D照射到a、b、c上三种光的频率关系，为，由光电效应的规律可知板b有电子射出，板c一定有光电子放出，正确答案为D

6．A航天飞机的运行周期

    设经过时间t航天飞机又通过建筑物上方，则

    ，所以

7．A沿着电场线的方向电势降低，，B错；E、F两点在同一等势面上，且，A正确

    由等量异种电荷的等势面特点可知．，C错，D错

8．C①F＝kA②

    由①②可知，C正确．

9．C先根据题意画出电子所走的弧，因为弧上任意一点的速度方向必然与该点所在的半径垂直，故可以过A点做与方向（即AB方向）垂直的直线，此即为带电粒子做匀速圆周运动的半径方向．同理过C点作垂直于BC的直线，也为该点的半径方向，两半径相交点即为带电粒子做匀速圆周运动的圆心．如答图1所示．由图示情况可以看出

答图1

    当时电子刚好不能从BC边射出．

    要使电子可以从BC边射出，必满足r＞，而r＝，

    ∴B＜时，电子可以从BC边射出

10．D11．（1）大于（2）轨道末端出口水平（3）P、、为落地的平均位置，F一步中的应为-2r，

12．（1）1.000

 （2）①略

    ②A．将滑动变阻器调至输出电压为零的位置，再合上．

    B．将扳向2，调滑动变阻器使电流表指针在某一电流刻度，并记下该位置．

    C．使阻值最大后，将扳向1，调电阻箱，使电流表指针回到所记的位置，记下电阻箱阻值．

    D．被测电阻＝．

13．侦察卫星环绕地球一周，通过有日照的赤道一次，在卫星一个周期时间（设为）地球自转的角度为q ，只要q 角所对应的赤道弧长能被拍摄下来，则一天时间内，地面上赤道处全部在有日照条件下就能被拍摄下来．设侦察卫量的周期为，地球对卫星的万有引力为卫星做圆周运动的向心力，卫星的轨道半径r＝R＋h，根据牛顿第二定律，则

    在地球表面的物体重力近似等于地球的万有引力，即mg＝

    解得侦察卫星的周期为

    已知地球自转周期为T，则卫星绕行一周，地球自转的角度为q ＝2p?

    摄像机应拍摄赤道圆周的弧长为q 角所对应的圆周弧长应为

14．当开关S在位置1时，粒子在电容器中做类平抛运动，即水平方向做匀速直线运动，竖直方向做初速度为零的匀加速直线运动，有

    l＝vt，

    得

    则带电粒子的初速度

    （m/s）

    当S接到2位置时，电容器内形成按余弦规律变化的振荡电场，周期为

    ．

    接到位置2时，电容器内电场仍竖直向上，设粒子在第一个内加速向下运动，在第二个内减速向下运动，在半个周期结束时，粒子的速度为零，平均加速度＜a，运动时间＜t，故粒子半个周期内竖直方向位移，粒子不会打到下极板上．

    在第三个内，粒子加速向上运动，在第四个内减速向上运动，在后半个周期结束时，粒子的速度为零．从对称性角度考虑，经过一个周期，粒子又回到两板中央，竖直方向速度为零．

    不论电容器内电场如何作用周期性的变化，粒子在水平方向不受电场力的作用，水平速度不变，所以粒子在电场中运动的时间仍为2×s，在这一时间内，电场做周期性变化的次数

    ．

    所以当粒子离开电容器时，竖直速度为零，水平速度不变，仍为v＝1.0×m/s，从两板中央飞出．

    所以粒子能飞出电容器，从两板中央水平飞出，v＝1.00×m/s．

15．（1）滑块速度向右，根据匀速运动条件

    ①

    可知E的方向必水平向右．

    由返回速度向左且作匀速运动可知

    ＝mg ②

    而题中有： ③

    ②③联立得知，即＝2mg，代入①式

    所以E＝m （mg＋2mg）/q＝3m mg/q

    （2）设往返总时间为T有：

    即：，代入②式可得

    （3）返回时不受摩擦力，所以全过程摩擦力做功

    W＝-fL＝-m （mg＋）L＝-3m mgL

16．用答图2示平面内的光线进行分析，并只讨论从右侧观察的情形，如图所示，由亮点发出的任一光线CP线经过两次折射而从液面射出．由折射定律，按图上标记的各相关角度．有sina ＝nsinb  ①

    sing ＝（1/n）sind ②

    其中d ≤p /2g ＝（p /2）-（b ＋j ） ③

答图2

    注意到，若液体内光线入射到液面上时发生全反射，就没有从液面射出的折射光线．全反射临界角满足条件sin＝1/n

    可知光线CP经折射后能从液面射出从而可被观察到的条件为g ＜④

    或sing ＜1/n⑤

    现在计算sing ．利用③式可得

    sing ＝cos（b ＋j ）＝cosb cosj -sinb sinj

    由①式可得cosb ＝

    因此，nsing ＝cosj -nsinb sinj 又由①式nsing＝cosj  -sina sinj  ⑥

    由图及①、②式，或由⑥式均可看出a 越大则g 越小，因此，如果与a 值最大的光线相应的g 设为，若＞，则任何光线都不能射出液面．反之，只要＜，这部分光线就能射出液面，从液面上方可以观察到亮点．由此极端情况即可求出本题要求的条件．

    自C点发出的a 值最大的光线是极靠近CD的光线，它被DB面折射后进入液体，由⑥式可知与之相应的

    a ＝（p /2）-j

    nsin＝cosj  -cosj sinj

    能观察到亮点的条件为nsin＜1

    即cosj -cosj sinj ＜1

    上式可写成cosj ＜1＋cosj sinj

    取平方

    化简

    故

    开方并化简可得

    这就是在液面上方从侧面适当的方向能看到亮点时n与j 之间应满足的条件．

17．（1）激光器的功率为＝NE①

    已知激光对物体表面的压力为F＝2N?p②

    由光压的定义 ③

    联立以上各式得④

    （2）太阳光对薄膜产生的光压

     ⑤

    探测器受到的总光压力

    F＝I?S⑥

    以探测器为研究对象，根据牛顿第二定律F＝m?a ⑦

    ^∴⑧

18．（1）由竖直上抛运动得炮弹被射出时的初速度①

    （2）由动量守恒定律得： ②

    带电物体在洛仑兹力作用下的直线运动是匀速直线运动，假设电场强度方向竖直向上，根据受力有：③

    ④

    联立②③④得：

    两物体匀速运动的速度

    ∴40m/s ⑤

    50m/s ⑥

    所加电场为

    _⑦

    因为E为正，所以场强方向竖直向上

    （3）由动能定理得：爆炸对两物体做的功

    _⑧

    _⑨

    （4）由平抛运动规律得落地时间：

    ⑩

    两物体的水平位移

    ＝＝40×4m＝160m

    ＝＝50×4m＝200m

    两物体落地点间的距离

    Ds＝＋＋L＝360＋20＝380m