练习册

  • 练习册
  • 试题
    图8 (1)这种电磁泵的原理是怎样的? (2)若导管内截面积为w×h.磁场的宽度为L.磁感应强度为B.液体穿过磁场区域的电流强度为I.如图8所示.求驱动力造成的压强差为多少? 【查看更多】

     

    题目列表(包括答案和解析)

    电磁炮是一种理想的兵器，它的主要原理如图8－1－19所示，利用这种装置可以把质量为m＝2.0 g的弹体(包括金属杆EF的质量)加速到6 km/s，若这种装置的轨道宽为d＝2 m，长L＝100 m，电流I＝10 A，轨道摩擦不计且金属杆EF与轨道始终接触良好，则下列有关轨道间所加匀强磁场的磁感应强度和磁场力的最大功率结果正确的是(　　)．

    A．B＝18 T，Pm＝1.08×108 W

    B．B＝0.6 T，Pm＝7.2×104 W

    C．B＝0.6 T，Pm＝3.6×106 W

    D．B＝18 T，Pm＝2.16×106 W

    查看答案和解析>>

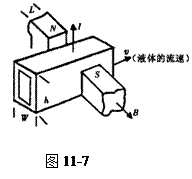    在原子反应堆中抽动液态金属和在医疗器械中抽动血液等导电液体时，由于不允许传动的机械部分与这些液体相接触，常使用一种电磁泵，如图11-7所示是这种电磁泵的结构，将导管放在磁场中，当电流穿过导电液体时，这种液体即被驱动，（1）这种电磁泵的原理是怎样的?___________________________________________________________________________________；

    （2）若导管内截面积为w×h，磁场的宽度为L，磁感应强度为B（看成匀强磁场），液体穿过磁场区域的电流强度为I，则驱动力造成的压强差为_____________．

    查看答案和解析>>

    如图8-2-1把重物G压在纸带上，用一水平力缓缓拉动纸带，重物跟着一起运动；若迅速拉动纸带，纸带将会从重物下抽出.解释这种现象的说法正确的是（    ）

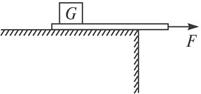
    图8-2-1

    A.在缓慢拉动纸带时，纸带给重物的摩擦力大

    B.在迅速拉动纸带时，纸带给重物的摩擦力小

    C.在缓慢拉动纸带时，纸带给重物的冲量大

    D.在迅速拉动纸带时，纸带给重物的冲量小

    查看答案和解析>>

    在原子反应堆中抽动液态金属和在医疗器械中抽动血液等导电液体时，由于不允许传动的机械部分与这些液体相接触，常使用一种电磁泵，如图11-7所示是这种电磁泵的结构，将导管放在磁场中，当电流穿过导电液体时，这种液体即被驱动，（1）这种电磁泵的原理是怎样的?______________________________________

    （2）若导管内截面积为w×h，磁场的宽度为L，磁感应强度为B（看成匀强磁场），液体穿过磁场区域的电流强度为I，则驱动力造成的压强差为_____________．

    查看答案和解析>>

    某同学用图8所示的装置来测定一玩具电动机在稳定状态下的输出功率.

    实验器材：玩具电动机，带有两个固定铁夹的铁架台，电磁打点计时器，低压交流电源，重锤，细线，米尺，纸带，复写纸片，天平等.

    实验步骤：

    图8

    ①将玩具电动机和电磁打点计时器固定在铁架台上，并与电源接好.

    把一根细线固定在电动机的转轮上，细线下端连接在重锤上端，将纸带的一端穿过打点计时器的限位孔后，固定在重锤上.

    ②起动玩具电动机带动重锤上升，同时接通打点计时器电源开始打点.

    ③经过一段时间，关闭打点计时器和电动机，取下纸带，进行测量.

    ④用天平测出重锤的质量.

    已知交流电源周期T=0.02s，当地的重力加速度为g=9.80m/s2，

    某次实验测得锤的质量为400.0g，得到的纸带的一段如图9所示.

    试回答下列问题：

    图9

    (1)由纸带上打下的点，可以判断重锤做_________运动.

    (2)由已知量和测得量求得玩具电动机的输出功率P=_________.

    (3)你认为玩具电动机的实际输出功率____________计算值(填“大于”、“等于”或“小于”).原因是：____________.

    查看答案和解析>>

    1．D；解析：电子从低轨道向高轨道跃迁，需要吸收能量，这些能量和一部分动能转化为电子与原子核的势能

    2．D；解析：的压缩量=（+）g/;的压缩量=g/；的伸长量'=g/；物块A上升的距离，物块B上升的距离

    3．D；解析：当两列波的平衡位置在P点相遇时，P的位移就不是最大了。

    4．A；解析：在M、N之间两者的场强方向都是向右的。由公式可知，因电量是4倍关系，则距离为2倍关系，两者场强大小才能相等。

    5．D；解析：合上K的瞬间，L对两灯并没有影响，A、B同时亮。稳定后，L相当于导线，A更亮，B熄灭，①③错，②对；稳定后断开K，L相当于瞬时电源，A灯没有电流，B灯有L提供的瞬时电流，所以，A熄灭，B重新亮后再熄灭，④对。

    6．A；解析：注意公式的条件（初速为零的匀变速的直线运动）。

    7．D；解析：③错在半衰期随温度变化。

    8．B；解析：光线入水到镜面，相当于白光进入三棱镜，折射后，光线分布是上红下紫。

    9．B；解析：根据公式和已知条件，可以求出B正确。

    10．B；解析：根据电磁感应的“阻碍”现象可以判断，两个线圈由于乙中电流变小而减小了吸引力，为了阻碍这个减小，甲中的电流应变大，又由于吸引力的作用，乙向左运动。

    11．0.483；3.517；3.034

    12．设计的电路：如答图1

    答图1

    13．不好（或不太好）

        根据电阻的定义：R＝知，U和I必须是电阻上的紧密关连的（或相互依存的）物理量，即：I必须是R两端电压降落为U值时，通过R的电流．

        如果先用伏特表测得待测电阻两端一个U值，后用电流表测得通过待测电阻的一个I值，对于一个确定的电源，由全电路欧姆定律知，测U时通过待测电阻的电流≠I，反之亦然．

    14．（1）工作原理：电流在磁场中受安培力

        （2）＝I?h?B　①

        　 ②

    15．（1）6×Wb；4×Wb

        （2）

       

       

       

        ∴　　

    16．设轻绳长为l．B　开始运动时的加速度

        当B开始运动，位移为l时，速度大小为

        相互作用结束时的共同速度为，根据动量守恒　

        则

        绳绷直后的加速度

        B的总位移为s时的共同速度为，则．

        由以上关系式解出　l＝0.25m

    17．两氘核进行对心碰撞，碰撞前后系统的动量守恒．碰撞前两氘核的动量之和为0，碰撞后设氦核和中子的动量分别是、，由动量守恒可得方程　

        题中说明核反应后所有结合能全部转化为机械能，则由能量守恒可得出核反应前后各粒子能量之间的关系式　由以上两方程再结合动量与动能之间的关系式便求得（1）问的解．

        （2）问中说明氦核沿直线向静止的核接近，就氦核和核组成的系统来说，因不受外力作用，故系统动量守恒．在库仑力作用下，两核距离最近时的物理意义是氦核和核的速度此时相等，因此可得一动量守恒方程．

        （1）反应中的质量亏损　＝2×2.0136-（3.0150＋1.0087）＝0.0035u

        所以释放的能量为　＝0.0035×931.5MeV＝3.26MeV

        设反应中生成的中子和氦核的速率分别为和由反应中能量守恒和动量守恒有

       

        其中＝0.35MeV

        由①得到

        所以动能之比为

        由②得到

        ∴　＝0.99MeV，＝2.97MeV

        （2）氦核与静止的碳核对心正碰后，当它们相距最近时，两核的速度相等，相当于完全非弹性碰撞模型，由动量守恒定律有　

        ∴　，此时，氦核的动能和碳核的动能分别为

        ≈0.04MeV

        ≈0.16MeV

    18．在板壁面上，分子碰后等速反弹，在Dt时间内，共有：个分子产生碰撞（为阿佛伽德罗常数）

        由动量定理，产生的冲力为：FDt＝（2mv）DN

        即：F＝，其中m ＝44g/mo1为的摩尔质量．

        ∴　压强

     

     

     

     

     


    同步练习册答案