
题目列表(包括答案和解析)
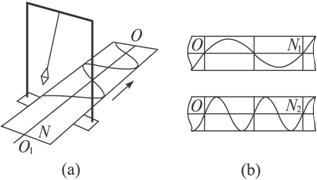
图
A.T2=T1 B.T2=2T
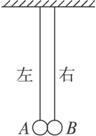
图
A.如果ma>mb,下一次碰撞将发生在平衡位置右侧
B.如果ma<mb,下一次碰撞将发生在平衡位置左侧
C.无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置右侧
D.无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置左侧
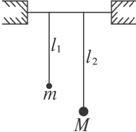
图
A.m的摆动周期几乎与M的周期相等
B.m的振幅随l1长短的改变而改变
C.l1=l2时,m有最大振幅
D.l1=l2时,m的振幅有可能大于M的振幅
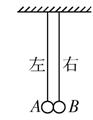
图
A.如果mA>mB,下一次碰撞将发生在平衡位置右侧
B.如果mA<mB,下一次碰撞将发生在平衡位置左侧
C.无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置右侧
D.无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置左侧
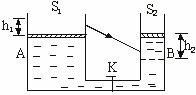
A.大气压对水做功,水的内能增加
B.水克服大气压力做功,水的内能减少
C.大气压力对水不做功,水的内能不变
D.大气压力对水不做功,水的内能增加
1.D 超导材料的电阻为零,因此只有D正确.
2.C 由玻尔理论可知.files/image103.gif) ,所以C正确.
,所以C正确.
3.B .files/image049.gif) 、
、.files/image051.gif) 并联与
并联与.files/image107.gif) 、
、.files/image109.gif) 的并联相串联,再与
的并联相串联,再与.files/image111.gif) 相并联,
相并联,.files/image113.gif) =0.5W,因此伏特表示数U=1.5V,安培表示数I=
=0.5W,因此伏特表示数U=1.5V,安培表示数I=
4.C 当B对地面恰无压力时,弹簧的伸长量.files/image115.gif) ,A达到最大速度时,弹簧的压缩量
,A达到最大速度时,弹簧的压缩量.files/image117.gif) ,此过程重力做功为
,此过程重力做功为.files/image119.gif)
5.D 同步卫星的加速度应为地球的自转角速度,所以a=.files/image029.gif) (R+h).
(R+h).
6.C .files/image122.gif) ∴
∴ .files/image124.gif) ,因此只有C正确.
,因此只有C正确.
7.B 利用平面镜成像规律,找到S的像点.files/image126.gif) ,确定垂直墙壁上的光斑,从而可知只有B正确.
,确定垂直墙壁上的光斑,从而可知只有B正确.
8.B 滑动变阻器用分压作用时,滑动变阻器阻值大的应为微调,阻值小的应为粗调,粗调时应选用.files/image049.gif) ,则
,则.files/image049.gif) 一定应为10W,
一定应为10W,.files/image051.gif) 一定应为200W,因此只有B正确.
一定应为200W,因此只有B正确.
9.D 金属块先加速后减速,最小速度为零,加速度先减小而后增大,因此C错;电场力始终做正功,电势能始终减小,因此B错;由能量守恒可知,电场力对金属块做的功应等于摩擦而产生的热量.
10.D 光线由O点射入,折射光线应靠近法线,即x轴光线射入材料后,法线应与y轴平行,入射角逐渐增大,当入射角大于临界角时,发生全反射,因此只有D正确.
11.(1)将.files/image066.gif) 接1,读出这时电压表和电流表的示数
接1,读出这时电压表和电流表的示数.files/image130.gif) 、
、.files/image132.gif)
(2).files/image134.gif)
12.答案:(1)甲
(2)①步骤B是错误的.应该接到电源的交流输出端.步骤D是错误的,应该先接通电源,待打点稳定后再释放纸带.步骤C不必要,因为根据测量原理,重锤的动能和势能中都包含了质量m,可以约去.
②.files/image136.gif)
③重锤的质量为m .files/image138.gif)
13.解析:(1)核方程.files/image140.gif)
设聚变后新核速度为V,中子速度为.files/image142.gif) ,质量为m,则由能量守恒定理得:
,质量为m,则由能量守恒定理得:
.files/image144.gif)
由动量守恒定律得:0=3mV+m.files/image142.gif) Dm=(2×2.01353u-3.015u-1.008665u)
Dm=(2×2.01353u-3.015u-1.008665u)
由以上各式可求得快中子动能 .files/image146.gif)
14.解析:a 粒子在水平方向做匀速运动 .files/image148.gif)
.files/image150.gif)
a 粒子在竖直方向做匀速运动 r=vt
解得 .files/image152.gif) B板发光面积S为
B板发光面积S为 .files/image154.gif)
15.解析:由F=.files/image156.gif) 得 小鸟:
得 小鸟:.files/image158.gif) 对飞机:
对飞机:.files/image160.gif)
得:.files/image162.gif)
∵ .files/image164.gif) =2as
=2as
∴ 跑道长至少为 .files/image166.gif) =
=
16.解析:(1)运动员从高处落下到接触沙坑表面的过程中,运动员重心下落的高度h=.files/image168.gif)
解得运动员落到地面的速度为v=.files/image170.gif) =
=
(2)运动员从下落到沙坑中停下,这个过程中初末动能都为零,重力做的功等于运动员克服沙坑阻力.files/image172.gif) 做的功,即 mg(h+l)=
做的功,即 mg(h+l)=.files/image174.gif)
得.files/image176.gif) 解得
解得 .files/image172.gif) =8.1×
=8.1×.files/image033.gif) N.
N.
17.解析:如答图1所示,设球的半径为R,在△OBP中
.files/image179.gif)
即.files/image181.gif)
.files/image183.jpg)
答图1
∴ i=45°
∠FOP=i-30°=45°-30°=15°
∵ 入射光线平行于MN
∴ ∠MOA=i=45°
由图知:
.files/image185.gif)
∴ .files/image187.gif) .
.
18.解析:(1)当回收舱在速度为.files/image172.gif) =0
=0
根据已知条件,得 .files/image189.gif) 解得: m=
解得: m=.files/image191.gif)
(2)在打开降落伞后,返回舱的加速度先增大而后减小,加速度方向向上,返回舱的速度不断减少,直到速度减小到
(3)反冲发动机工作后,使回收舱的速度由.files/image193.gif)
解得 F=9.9×.files/image195.gif) N.
N.
反冲发动机对返回舱做的功W=Fh=1.2×.files/image197.gif) J.
J.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com