
题目列表(包括答案和解析)

A.质点A B.质点B C.质点C D.质点D
一列简谐横波沿x轴负方向传播,a、b、c、d为介质中沿波传播方向上四个质点 的平衡位置。某时刻的波形如图甲所示,此后,若经过四分之三个周期开始计时,则图乙 描述的是
A. a处质点的振动图像
B. b处质点的振动图像
C. c处质点的振动图像
D. d处质点的振动图像

一列简谐横波沿x轴负方向传播,a、b、c、d为介质中沿波传播方向上四个质点 的平衡位置。某时刻的波形如图甲所示,此后,若经过四分之三个周期开始计时,则图乙 描述的是
A. a处质点的振动图像
B. b处质点的振动图像
C. c处质点的振动图像
D. d处质点的振动图像
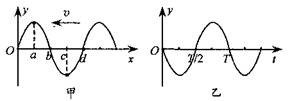
一列横波沿x轴负向传播,a、b、c、d为介质中沿波传播方向上四个质点的平衡位置,某时刻波形如图甲所示,此后若经过半个周期开始计时,则图乙描述的是
A.a质点振动图象 B.b质点振动图象
C.c质点振动图象 D.d质点振动图象
一列横波沿x轴负向传播,a、b、c、d为介质中沿波传播方向上四个质点的平衡位置,某时刻波形如图甲所示,此后若经过半个周期开始计时,则图乙描述的是
A.a质点振动图象 B.b质点振动图象
C.c质点振动图象 D.d质点振动图象
一、本题共10小题,每小题4分,共40分。在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确。全部选对的得4分,选不全的得2分,有选错的或不答得0分。
1、D 根据重力的定义;重力的测量只能用弹簧测力计。
2、B、C、D 合力与分力是从力的作用效果相同来考虑的。
3、B、D B加速上升处于超重状态。
4、C VAB=(VA+VB)/2,VBC=(VB+VC)/2,VAC=(VA+VC)/2。可求出VAC
5、B、D
6、A 两导线受力具有对称性。
7、B 分别对m、M进行研究,刚开始时,F1>F弹,F2>F弹,m、M速度都增加,为一加速过程,直到a=0时,速度不再增加,但由于惯性,它们分别都要向前运动,所以速度又要减少,直到其中一个速度为0,然后反向,所以C错。B 对。
8、BCD 由R1、R2串联分压可求R1、R2两端电压分别为2.4V、3.6V,当电压表与R1并联时RVR1/(RV+R1):R2=2:4,解得RV=6 kΩ,当电压表与R2并联时,其等效电阻2 kΩ,其两端电压应为3V。
9、BD 由乙图可知质点从平衡位置的正方向运动。
10、B
二、本题共8小题,共110分。按题目要求作答。解答题应写出必要条件的文字说明、方程式和重要演算步骤。只写出最后答案的不能得分。有数值计算的题,答案中必须明确写出数值和单位。
11.(1)
(2)(a)
12.(1).files/image039.gif)
.files/image040.gif) (2)
(2).files/image042.gif)
13.(1)R1
(2)电路图如右图所示
(3)E=1.47 (1.46~1.48均对),
r=0.83 (0.81~0.85均可以)
14、(1)极板间的电场强度E=U/d
(2)α粒子电荷为2e,质量为
(3)由d=at2/2,得:t= v=R/t
15、物体在地球表面时,G=mg;在卫星离地高H时,F-G‘=ma,G‘=mg’
而g/g‘=(R+H)2/R2
H=1.92x
16、设两球之间的斥力大小是F,两球从开始相互作用到两球相距最近时所经历的时间是t。当两球相距最近时球B的速度VB=
由动量守恒定律可得:mBVB0=mAVA+mBVB
得:VB0=9m/s
(2)两球从开始相互作用到它们之间距离最近时,它们之间的相对位移ΔS=L-d,由功能关系可得:FΔS=mBV2B0/2-(mAV2A/2+mBV2B/2)
得:F=2.25N
(3)根据动量定理,对A球有Ft=mVA-0,t=mAVA/F=32/9=3.56s
17、(2)由几何关系求出粒子在磁场中做匀速运动的半径:r2=202+(40-r)2
.files/image044.jpg) 又因:Bqv=mv2/r, 而EK=mv2/2
又因:Bqv=mv2/r, 而EK=mv2/2
可求得:B=8.0×10-2T
(3)由图可知Sinθ=15/25=3/5故θ=370,粒子在磁场中做匀速圆周运动,则到P点时转过的圆心角为:φ=θ+900=1270
粒子从0点运动到P点所用的时间为:t=φT/3600,其中T=2Лm/Bq
t=5.54×10-7s
18、(1)设棒第一次上升过程中,环的加速度为a1,环受合力F=kmg-mg,由牛顿第二定律F=ma1。由两式得:a1=(k-1)g,方向竖直向上。
(2)设以地面为零势能面,向上为正方向棒第一次落地的速度大小为v1,由机械能守恒可得:v12=2gH
设棒弹起后的加速度为a2,由牛顿第二定律:a2=-(k+1)g
棒第一次弹起的最大高度为:H1=-v1/2a2
得:H1=H/(k+1),棒运动的路程为:S=H+2H1=(k+3)H/(k+1)
(3)设环相对棒滑动距离为L,根据能量守恒:mgH+mg(H+L)=kmgL,
摩擦力对棒及环做的总功:W=-kmgL
解得:W=-2kmgH/(k-1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com