
题目列表(包括答案和解析)
| A.①和② | B.①和③ | C.②和④ | D.③和④ |
设 、
、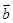 、
、 为同平面内具有相同起点的任意三个非零向量,且满足
为同平面内具有相同起点的任意三个非零向量,且满足 与
与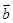 不共线,
不共线,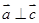 ,
, ,则
,则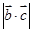 的值一定等于( )
的值一定等于( )
A.以 、
、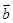 为两边的三角形面积; B.以
为两边的三角形面积; B.以 、
、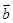 为邻边的平行四边形的面积;
为邻边的平行四边形的面积;
C.以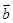 、
、 为两边的三角形面积; D.以
为两边的三角形面积; D.以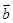 、
、 为邻边的平行四边形的面积.
为邻边的平行四边形的面积.
设 、
、 、
、 为同平面内具有相同起点的任意三个非零向量,且满足
为同平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线,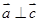 ,
, ,则
,则 的值一定等于( )
的值一定等于( )
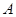 .以
.以 、
、 为两边的三角形面积;
为两边的三角形面积;  .以
.以 、
、 为邻边的平行四边形的面积;
为邻边的平行四边形的面积;
C.以 、
、 为两边的三角形面积;
为两边的三角形面积;  .以
.以 、
、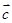 为邻边的平行四边形的面积
为邻边的平行四边形的面积
一、选择题:
A卷:CCABD BDCBB AA
二、填空题:
(13).files/image310.gif) (14)
(14).files/image312.gif) (15)
(15).files/image314.gif) (16)
(16) .files/image316.gif)
三、解答题:
(17)解:
(Ⅰ)由.files/image318.gif) ,得
,得.files/image320.gif) , ∴
, ∴.files/image322.gif)
又.files/image324.gif) ,即
,即.files/image326.gif) ,得
,得.files/image328.gif) ……………4分
……………4分
(Ⅱ)当.files/image330.gif) 时,
时,.files/image332.gif) ,
,
得.files/image334.gif) ,即
,即.files/image336.gif) ,…………………………7分
,…………………………7分
由.files/image338.gif) 知,
知,.files/image340.gif)
.files/image237.gif) ,
,
∴.files/image343.gif) ,
,.files/image230.gif) 是首项为
是首项为.files/image346.gif) ,公比为
,公比为.files/image346.gif) 的等比数列,
的等比数列,
∴.files/image349.gif) ……………………………………………………10分
……………………………………………………10分
(18)解:
由.files/image247.gif) ,知
,知.files/image352.gif) ,又
,又.files/image245.gif) ,由正弦定理,有
,由正弦定理,有
.files/image355.gif) ,∴
,∴.files/image357.gif) ,
,.files/image359.gif) ,……3分
,……3分
∴.files/image361.gif) ……………6分
……………6分
.files/image363.gif)
.files/image365.gif) …………9分
…………9分
∵.files/image367.gif) ,
,.files/image369.gif) , ∴
, ∴.files/image371.gif) ,
,
故所求函数为.files/image373.gif)
.files/image375.gif) ,函数的值域为
,函数的值域为.files/image377.gif) ……………12分
……………12分
(19)解:
记顾客购买一件产品,获一等奖为事件.files/image379.gif) ,获二等奖为事件
,获二等奖为事件.files/image381.gif) ,不获奖为事件
,不获奖为事件.files/image383.gif) ,则
,则.files/image385.gif) ,
,.files/image387.gif) ,
,.files/image389.gif)
(Ⅰ)该顾客购买2件产品,中奖的概率
.files/image391.gif) ……………4分
……………4分
(Ⅱ)该顾客获得奖金数不小于100元的可能值为100元,120元,200元,依次记这三个事件为.files/image393.gif) 、
、.files/image395.gif) 、
、.files/image397.gif) ,则
,则
.files/image399.gif) ,………6分
,………6分
.files/image401.gif) ,………8分
,………8分
.files/image403.gif) ,………10分
,………10分
所以该顾客获得奖金数不小于100元的概率
.files/image405.gif) ……12分
……12分
(20)解法一:
(Ⅰ)取.files/image407.gif) 中点
中点.files/image409.gif) ,连结
,连结.files/image411.gif) 、
、.files/image413.gif) ,则
,则.files/image415.gif) ,
,
又.files/image417.gif) ,
∴
,
∴.files/image419.gif) ,四边形
,四边形.files/image421.gif) 是平行四边形,
是平行四边形,
∴.files/image423.gif) ,又
,又.files/image425.gif) ,
,.files/image427.gif) ,
,
∴.files/image278.gif) ……………………………………………………4分
……………………………………………………4分
(Ⅱ)连结.files/image430.gif)
∵.files/image432.gif) , ∴
, ∴.files/image434.gif) ,
,
又平面.files/image436.gif) 平面
平面.files/image262.gif) ,∴
,∴.files/image439.gif)
而.files/image441.gif) , ∴
, ∴.files/image443.gif)
作.files/image445.gif) 于
于.files/image447.gif) ,则
,则.files/image449.gif) ,且
,且.files/image451.gif) ,
,.files/image447.gif) 为
为.files/image454.gif) 的中点。
的中点。
作.files/image456.gif) 于
于.files/image458.gif) ,连结
,连结.files/image460.gif) ,则
,则.files/image462.gif) ,
,
于是.files/image464.gif) 为二面角
为二面角.files/image280.gif) 的平面角。…………………………8分
的平面角。…………………………8分
∵.files/image266.gif) ,
,.files/image268.gif) ,∴
,∴.files/image469.gif) ,
,.files/image471.gif)
在正方形.files/image262.gif) 中,作
中,作.files/image474.gif) 于
于.files/image476.gif) ,则
,则
.files/image478.gif) ,
,
∴.files/image480.gif) ,∴
,∴.files/image482.gif) 。
。
故二面角.files/image280.gif) 的大小为
的大小为.files/image485.gif) …………………………12分
…………………………12分
.files/image487.jpg) |
解法二:如图,以.files/image270.gif) 为原点,建立空间直角坐标系,使
为原点,建立空间直角坐标系,使.files/image490.gif) 轴,
轴,.files/image002.gif) 、
、.files/image493.gif) 分别在
分别在.files/image070.gif) 轴、
轴、.files/image496.gif) 轴上。
轴上。
(Ⅰ)由已知,.files/image498.gif) ,
,.files/image500.gif) ,
,.files/image502.gif) ,
,.files/image504.gif) ,
,.files/image506.gif) ,
,.files/image508.gif) ,
,
∴.files/image510.gif) ,
,
.files/image512.gif) ,
,.files/image514.gif) ,
,
∵.files/image516.gif) ,
∴
,
∴.files/image518.gif) ,
,
又.files/image520.gif) ,∴
,∴.files/image278.gif) ………………………………………4分
………………………………………4分
(Ⅱ)设.files/image523.gif) 为面
为面.files/image525.gif) 的法向量,则
的法向量,则.files/image527.gif) ,且
,且.files/image529.gif) 。
。
∵.files/image531.gif) ,
,.files/image510.gif) ,
,.files/image534.gif)
∴.files/image536.gif) ,取
,取.files/image538.gif) ,
,.files/image540.gif) ,
,.files/image542.gif) ,则
,则.files/image544.gif) ……………8分
……………8分
又.files/image546.gif) 为面
为面.files/image548.gif) 的法向量,所以
的法向量,所以.files/image550.gif) ,
,
因为二面角.files/image280.gif) 为锐角,所以其大小为
为锐角,所以其大小为.files/image553.gif) …………………………12分
…………………………12分
(21)解:
(Ⅰ).files/image555.gif)
令.files/image557.gif) ,
,.files/image559.gif) ,则
,则.files/image561.gif) ………………2分
………………2分
若.files/image563.gif) ,即
,即.files/image565.gif) ,则恒有
,则恒有.files/image567.gif) ,函数
,函数.files/image112.gif) 没有极值点。…………4分
没有极值点。…………4分
若.files/image570.gif) ,即
,即.files/image572.gif) ,或
,或.files/image574.gif) ,则
,则.files/image557.gif) 有两个不相等的实根
有两个不相等的实根.files/image287.gif) 、
、.files/image289.gif)
.files/image578.gif) ,且
,且.files/image580.gif) 的变化如下:
的变化如下:
.files/image068.gif)
.files/image583.gif)
.files/image585.gif)
.files/image587.gif)
.files/image289.gif)
.files/image590.gif)
.files/image580.gif)
.files/image593.gif)
.files/image028.gif)
-
.files/image028.gif)
.files/image593.gif)
由此,.files/image596.gif) 是函数
是函数.files/image112.gif) 的极大值点,
的极大值点,.files/image599.gif) 是函数
是函数.files/image112.gif) 的极小值点。
的极小值点。
综上所述,.files/image284.gif) 的取值范围是
的取值范围是.files/image603.gif) …………………………7分
…………………………7分
(Ⅱ)由(Ⅰ)知,.files/image605.gif) ,
,.files/image607.gif) ,
,
∴.files/image609.gif)
.files/image611.gif)
.files/image613.gif)
.files/image615.gif) …………………………10分
…………………………10分
令.files/image617.gif) ,得
,得.files/image619.gif) (舍去),
(舍去),.files/image621.gif) ,
,.files/image623.gif)
所以,.files/image625.gif) 或
或.files/image627.gif) …………………………12分
…………………………12分
(22)解:
(Ⅰ)记
.files/image629.gif) ①
①
.files/image631.gif) ②
②
②.files/image633.gif) ,得
,得
.files/image635.gif) ,
③
,
③
由①、③,得.files/image637.gif) ,即
,即.files/image639.gif) ……3分
……3分
由于.files/image641.gif) ,
,.files/image643.gif) ,则上面方程可化为
,则上面方程可化为
.files/image645.gif) ,即
,即.files/image647.gif) ,所以
,所以.files/image649.gif) ,
,
将.files/image649.gif) 代入①式,整理,并注意
代入①式,整理,并注意.files/image652.gif) ,得
,得.files/image654.gif)
由于.files/image656.gif) ,所以
,所以.files/image658.gif)
因此,直线.files/image298.gif) 与双曲线
与双曲线.files/image204.gif) 有一个公共点
有一个公共点.files/image018.gif) …………………………6分
…………………………6分
(注:直线和双曲线联立后,利用.files/image663.gif) 判断交点个数也可)
判断交点个数也可)
(Ⅱ)双曲线.files/image204.gif) 的渐近线方程为
的渐近线方程为.files/image666.gif) ,不妨设点
,不妨设点.files/image002.gif) 在直线
在直线.files/image669.gif) 上,
点
上,
点.files/image004.gif) 在直线
在直线.files/image672.gif) 上。
上。
由.files/image674.gif) ,得点
,得点.files/image002.gif) 坐标为
坐标为.files/image676.gif) ,
,
由.files/image678.gif) ,得点
,得点.files/image004.gif) 坐标为
坐标为.files/image681.gif) ,…………………………9分
,…………………………9分
因为.files/image683.gif) ,
,.files/image685.gif)
所以.files/image018.gif) 为线段
为线段.files/image274.gif) 的中点。…………………………12分
的中点。…………………………12分
(注:若只计算.files/image002.gif) 、
、.files/image004.gif) 的横坐标或纵坐标判断
的横坐标或纵坐标判断.files/image018.gif) 为线段
为线段.files/image274.gif) 的中点不扣分)
的中点不扣分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com