
题目列表(包括答案和解析)
已知函数 对任意实数x均有
对任意实数x均有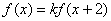 ,其中常数k为负数,且
,其中常数k为负数,且 在区间[0,2]上有表达式
在区间[0,2]上有表达式
(1)求 的值;
的值;
(2)写出 在[-3,3]上的表达式,并讨论函数
在[-3,3]上的表达式,并讨论函数 在[-3,3]上的单调性;
在[-3,3]上的单调性;
(3)求出 在[-3,3]上的最小值与最大值,并求出相应的自变量的取值.
在[-3,3]上的最小值与最大值,并求出相应的自变量的取值.
| π |
| 3 |
| β |
| 2 |
(本小题满分14分)
已知函数 对任意实数
对任意实数 均有
均有 ,其中常数
,其中常数 为负数,且
为负数,且 在区间
在区间 上有表达式
上有表达式 .
.
(1)求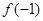 ,
, 的值;
的值;
(2)写出 在
在 上的表达式,并讨论函数
上的表达式,并讨论函数 在
在 上的单调性;
上的单调性;
(3)求出 在
在 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
 .
.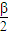 是第几象限的角?
是第几象限的角?题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
A
A
B
B
D
C
B
B
C
13.
9 14.  15.
15.  16.
16. 
17.解:(1)
 (4分)
(4分)
 的最小正周期为
的最小正周期为 (5分)
(5分)
 的最小值为-2
(6分)
的最小值为-2
(6分)
(2) 的递增区间为
的递增区间为 和
和 (10分)
(10分)
18.(1)证明:过D作DH AE于H,
AE于H,
 平面ADE
平面ADE 平面ABCE
平面ABCE
 DH
DH 平面ABCE
平面ABCE  DH
DH BE
BE
在 中,由题设条件可得:AB=2,AE=BE=
中,由题设条件可得:AB=2,AE=BE=
 AE
AE BE
BE
 BE
BE 平面ADE
(6分)
平面ADE
(6分)
(2)由(1)知,BE 平面ADE,
平面ADE,
 为BD和平面ADE所成的角,且BE
为BD和平面ADE所成的角,且BE DE
DE
 在矩形ABCD中,AB=2,AD=1,E为CD的中点
在矩形ABCD中,AB=2,AD=1,E为CD的中点
 DE=1,BE=
DE=1,BE=
在 中,
中,
故BD和平面ADE所成角的正切值为 (12分)
(12分)
19.(1)记“3粒种子,至少有1粒未发芽”为事件 ,
,
由题意,种3粒种子,相当于作3次独立重复试验,
故 (4分)
(4分)
(2)记“3粒A种子,至少有2粒未发芽”为事件 ,“3粒B种子,全部发芽”为事件
,“3粒B种子,全部发芽”为事件 ,则
,则
 (6分)
(6分)
由于 相互独立,故
相互独立,故 (8分)
(8分)
(3) (12分)
(12分)
20.解:(1) 的图像关于原点对称,
的图像关于原点对称, 为奇函数
为奇函数
 又
又
 (4分)
(4分)
(2)假设存在两点 满足题设条件
满足题设条件



 而两切线垂直,则应有
而两切线垂直,则应有 ,矛盾,
,矛盾,
故不存在满足题设条件的两点A,B (8分)
(3) 时,
时, ,
, 在
在 为减函数
为减函数
 而
而 时
时
 (12分)
(12分)
21.解:(1)
两式相减得:
又 时,
时,
 是首项为
是首项为 ,公比为
,公比为 的等比数列
的等比数列
 (4分)
(4分)
(2)
 为以-1为公差的等差数列,
为以-1为公差的等差数列, (7分)
(7分)
(3)

以上各式相加得:
当 时,
时,

当 时,上式也成立,
时,上式也成立, (12分)
(12分)
22.(1)依抛物线定义知,点P的轨迹C,为N,F为焦点,直线 为准线的抛物线
为准线的抛物线
曲线C的方程为 .
(4分)
.
(4分)
(2)①设M、N的方程为 带入
带入 并整理得
并整理得

设MN的中点为 则
则
 MN的垂直平分线方程为
MN的垂直平分线方程为
 点B的坐标为
点B的坐标为
 故
故 的范围是
的范围是 (8分)
(8分)
②易得弦长
若 为直角三角形,则为等腰直角三角形,
为直角三角形,则为等腰直角三角形,
 点B的坐标为(0,10)
点B的坐标为(0,10)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com