练习册

  • 练习册
  • 试题
    由题设知 【查看更多】

     

    题目列表(包括答案和解析)

    设数列{an}是由1，2，3，4，5这5个数字组成无重复数字的五位数按从小到大的顺序排列得到的．

    (1)已知an＝54321，求n；

    (2)求a96；

    (3)已知am＝45132，求m；

    (4)求Sn．

    查看答案和解析>>

    设事件A发生的概率为P，若在A发生的条件下B发生的概率为P′，则由A产生B的概率为PP′，根据这一规律解答下题：一种掷硬币走跳棋的游戏：棋盘上有第0，1，2，3，…，100，共101站，设棋子跳到第n站的概率为Pn，一枚棋子开始在第0站（即P0=1），由棋手每掷一次硬币，棋子向前跳动一次，若硬币出现正面则棋子向前跳动一站，出现反面则向前跳动两站，直到棋子跳到第99站（获胜）或100站（失败）时，游戏结束．已知硬币出现正反面的概率都为
    12
    ．
    （1）求P1，P2，P3，并根据棋子跳到第n+1站的情况，试用Pn，Pn-1表示Pn+1；
    （2）设an=Pn-Pn-1（1≤n≤100），求证：数列{an}是等比数列，并求出{an}的通项公式；
    （3）求玩该游戏获胜的概率．

    查看答案和解析>>

    设函数
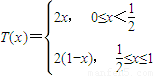
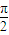    （1）求函数y=T（sin（x））和y=sin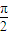（T（x））的解析式；
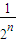    （2）是否存在非负实数a，使得aT（x）=T（ax）恒成立，若存在，求出a的值；若不存在，请说明理由；
    （3）定义Tn+1（x）=Tn（T（x）），且T1（x）=T（x），（n∈N*）
    ①当x∈[0，]时，求y=Tn（x）的解析式；
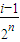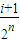    已知下面正确的命题：当x∈[，]（i∈N*，1≤i≤2n-1）时，都有Tn（x）=Tn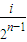（-x）恒成立．
    ②对于给定的正整数m，若方程Tm（x）=kx恰有2m个不同的实数根，确定k的取值范围；若将这些根从小到大排列组成数列{xn}（1≤n≤2m），求数列{xn}所有2m项的和．

    查看答案和解析>>

    设函数
    （1）求函数y=T（x2）和y=（T（x））2的解析式；
    （2）是否存在实数a，使得T（x）+a2=T（x+a）恒成立，若存在，求出a的值，若不存在，请说明理由；
    （3）定义Tn+1（x）=Tn（T（x）），且T1（x）=T（x），（n∈N*）
    ①当时，求y=T4（x）的解析式；
    已知下面正确的命题：当时（i∈N*，1≤i≤15），都有恒成立．
    ②若方程T4（x）=kx恰有15个不同的实数根，确定k的取值；并求这15个不同的实数根的和．

    查看答案和解析>>

    设是两个不共线的非零向量.

    （1）若=，=，=，求证：A，B，D三点共线；

    （2）试求实数k的值，使向量和共线. (本小题满分13分)

    【解析】第一问利用=（）+（）+==得到共线问题。

    第二问，由向量和共线可知

    存在实数，使得=()

    =，结合平面向量基本定理得到参数的值。

    解：（1）∵=（）+（）+

    ==    ……………3分

    ∴      ……………5分

    又∵∴A，B，D三点共线   ……………7分

    （2）由向量和共线可知

    存在实数，使得=()   ……………9分

    ∴=   ……………10分

    又∵不共线

    ∴  ……………12分

    解得

     

    查看答案和解析>>


    同步练习册答案