
题目列表(包括答案和解析)
为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间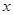 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为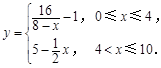 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(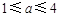 )个单位的药剂,要使接下来的4天中能够持续有效净化,试求
)个单位的药剂,要使接下来的4天中能够持续有效净化,试求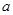 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: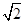 取1.4).
取1.4).
 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用. )个单位的药剂,要使接下来的4天中能够持续有效净化,试求
)个单位的药剂,要使接下来的4天中能够持续有效净化,试求 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: 取1.4).
取1.4).选择题.
(1)
由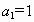 ,
,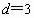 确定的等差数列
确定的等差数列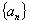 ,当
,当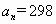 时,序号n等于
时,序号n等于
[
]|
(A)99 . |
(B)100 . |
(C)96 . |
(D)101 . |
(2)
一个蜂巢里有1只蜜蜂.第1天,它飞出去找回了5个伙伴;第2天,6只蜜蜂飞出去,各自找回了5个伙伴……如果这个找伙伴的过程继续下去,第6天所有的蜜蜂都归巢后,蜂巢中一共有( )只蜜蜂.[
]|
(A)55986 . |
(B)46656 . |
(C)216 . |
(D)36 . |
(3)
预测人口的变化趋势有多种方法,“直接推算法”使用的公式是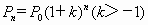 ,其中
,其中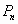 为预测期人口数,
为预测期人口数,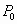 为初期人口数,k为预测期内年增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么在这期间人口数
为初期人口数,k为预测期内年增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么在这期间人口数
[
]|
(A) 呈上升趋势. |
(B) 呈下降趋势. |
(C) 摆动变化. |
(D) 不变. |
(4)
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的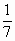 是较小的两份之和,问最小1份为
是较小的两份之和,问最小1份为
[
]|
(A) |
(B) |
(C) |
(D) |
某公司全年的利润为b元,其中一部分作为奖金发给n位职工,奖金分配方案如下:首先将职工按工作业绩(工作业绩均不相同)从大到小,由1到n排序,第一位职工得奖金![]() 元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
(1)设ak(1≤k≤n)为第k位职工所得奖金额,试求a2、a3,并用k、n和b表示ak(不必证明);
(2)证明ak>ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义;
(3)发展基金与n和b有关,记为Pn(b),对常数b,当n变化时,求![]() Pn(b)
Pn(b)
某公司全年的利润为b元,其中一部分作为奖金发给n位职工,奖金分配方案如下:首先将职工按工作业绩(工作业绩均不相同)从大到小,由1到n排序,第1位职工得奖金![]() 元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
(1)设ak(1≤k≤n)为第k位职工所得奖金金额,试求a2、a3,并用k、n和b表示ak(不必证明);
(2)证明ak>ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义;
(3)发展基金与n和b有关,记为Pn(b),对常数b,当n变化时,求![]() Pn(b).
Pn(b).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com