
题目列表(包括答案和解析)
如图,已知抛物线 :
: 和⊙
和⊙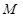 :
: ,过抛物线
,过抛物线 上一点
上一点 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点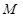 到抛物线准线的距离为
到抛物线准线的距离为 .
.

(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)当 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线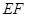 的斜率;
的斜率;
(Ⅲ)若直线 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值.
如图,已知抛物线 :
: 和⊙
和⊙ :
: ,过抛物线
,过抛物线 上一点
上一点 作两条直线与⊙
作两条直线与⊙ 相切于
相切于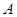 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 到抛物线准线的距离为
到抛物线准线的距离为 .
.

(1)求抛物线 的方程;
的方程;
(2)当 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线 的斜率;
的斜率;
(3)若直线 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值.
如图,已知抛物线 :
: 和⊙
和⊙ :
: ,过抛物线
,过抛物线 上一点
上一点 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 到抛物线准线的距离为
到抛物线准线的距离为 .
.

(1)求抛物线 的方程;
的方程;
(2)当 的角平分线垂直轴时,求直线
的角平分线垂直轴时,求直线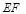 的斜率;
的斜率;
(3)若直线 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值.
如图,已知抛物线 :
: 和⊙
和⊙ :
: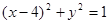 ,过抛物线
,过抛物线 上一点
上一点 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、 两点,分别交抛物线于
两点,分别交抛物线于 两点,圆心点
两点,圆心点 到抛物线准线的距离为
到抛物线准线的距离为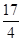 .
.

(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)当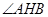 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线 的斜率;
的斜率;
(Ⅲ)若直线 在
在 轴上的截距为
轴上的截距为 ,求
,求 的最小值.
的最小值.
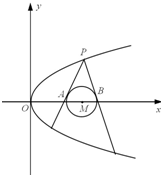 (2013•杭州一模)已知抛物线C:y2=2px(p>0)和⊙M:x2+y2+8x-12=0,过抛物线C上一点P(x0,y0)(y0≥0)作两条直线与⊙M相切与A、B两点,圆心M到抛物线准线的距离为
(2013•杭州一模)已知抛物线C:y2=2px(p>0)和⊙M:x2+y2+8x-12=0,过抛物线C上一点P(x0,y0)(y0≥0)作两条直线与⊙M相切与A、B两点,圆心M到抛物线准线的距离为| 9 |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com