
题目列表(包括答案和解析)
已知函数![]() 的图像是自原点出发的一条折线,当
的图像是自原点出发的一条折线,当![]() 时,该图像是斜率为
时,该图像是斜率为![]() 的线段(其中正常数
的线段(其中正常数![]() ),设数列
),设数列![]() 由
由![]() 定义.
定义.
Ⅰ.求![]() 、
、![]() 和
和![]() 的表达式;
的表达式;
Ⅱ.求![]() 的表达式,并写出其定义域;
的表达式,并写出其定义域;
Ⅲ.证明:![]() 的图像与
的图像与![]() 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点.
函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
(1)求实数a,b,并确定函数 的解析式;
的解析式;
(2)判断 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
【解析】本试题主要考查了函数的解析式和奇偶性和单调性的综合运用。第一问中,利用函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
解得 ,
,
(2)中,利用单调性的定义,作差变形判定可得单调递增函数。
(3)中,由2知,单调减区间为 ,并由此得到当,x=-1时,
,并由此得到当,x=-1时, ,当x=1时,
,当x=1时,
解:(1) 是奇函数,
是奇函数, 。
。
即 ,
, ,
, ………………2分
………………2分
 ,又
,又 ,
, ,
, ,
,
(2)任取 ,且
,且 ,
,
 ,………………6分
,………………6分
 ,
,
 ,
, ,
, ,
, ,
,
 在(-1,1)上是增函数。…………………………………………8分
在(-1,1)上是增函数。…………………………………………8分
(3)单调减区间为 …………………………………………10分
…………………………………………10分
当,x=-1时, ,当x=1时,
,当x=1时, 。
。
已知函数![]() 的图象是自原点出发的一条折线.当
的图象是自原点出发的一条折线.当![]() 时,该图象是斜率为
时,该图象是斜率为![]() 的线段(其中正常数
的线段(其中正常数![]() ),设数列
),设数列![]() 由
由![]() 定义. 求:
定义. 求:
求![]() 和
和![]() 的表达式;
的表达式;
求![]() 的表达式,并写出其定义域;
的表达式,并写出其定义域;
证明:![]() 的图像与
的图像与![]() 的图象没有横坐标大于1的交点.
的图象没有横坐标大于1的交点.
A
解析:由题意:等比数列{![]() }有连续四项在集合{-54,-24,18,36,81}中,由等比数列的定义知,四项是两个正数,两个负数且|q|>1,故-24, 36, -54,81符合题意,则q=
}有连续四项在集合{-54,-24,18,36,81}中,由等比数列的定义知,四项是两个正数,两个负数且|q|>1,故-24, 36, -54,81符合题意,则q=![]() ,6q=-9.
,6q=-9.
如图, 是△
是△ 的重心,
的重心, 、
、 分别是边
分别是边 、
、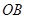 上的动点,且
上的动点,且 、
、 、
、 三点共线.
三点共线.
(1)设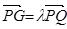 ,将
,将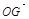 用
用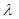 、
、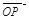 、
、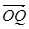 表示;
表示;
(2)设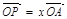 ,
,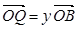 ,证明:
,证明: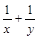 是定值;
是定值;
(3)记△ 与△
与△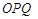 的面积分别为
的面积分别为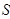 、
、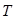 .求
.求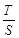 的取值范围.
的取值范围.
(提示: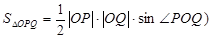
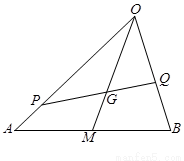
【解析】第一问中利用(1)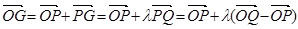
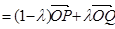
第二问中,由(1),得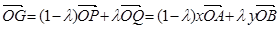 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴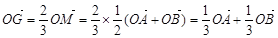
而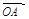 、
、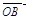 不共线,∴由①、②,得
不共线,∴由①、②,得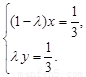
第三问中,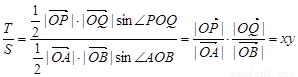
由点 、
、 的定义知
的定义知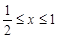 ,
,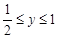 ,
,
且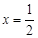 时,
时,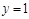 ;
;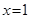 时,
时,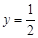 .此时,均有
.此时,均有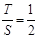 .
.
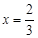 时,
时,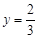 .此时,均有
.此时,均有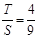 .
.
以下证明: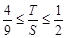 ,结合作差法得到。
,结合作差法得到。
解:(1)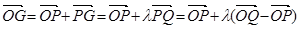
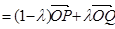 .
.
(2)一方面,由(1),得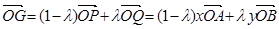 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴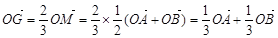 . ②
. ②
而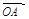 、
、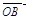 不共线,∴由①、②,得
不共线,∴由①、②,得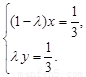
解之,得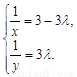 ,∴
,∴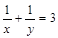 (定值).
(定值).
(3)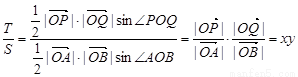 .
.
由点 、
、 的定义知
的定义知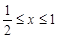 ,
,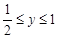 ,
,
且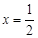 时,
时,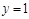 ;
;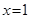 时,
时,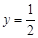 .此时,均有
.此时,均有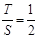 .
.
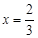 时,
时,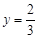 .此时,均有
.此时,均有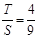 .
.
以下证明: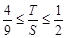 .(法一)由(2)知
.(法一)由(2)知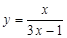 ,
,
∵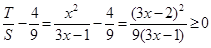 ,∴
,∴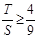 .
.
∵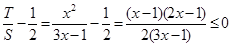 ,∴
,∴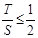 .
.
∴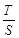 的取值范围
的取值范围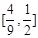
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com