
题目列表(包括答案和解析)
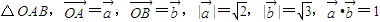 ,边AB上一点P1,这里P1异于A、B.由P1引边OB的垂线P1Q1,Q1是垂足,再由Q1引边OA的垂线Q1R1,R1是垂足.又由R1引边AB的垂线R1P2,P2是垂足.同样的操作连续进行,得到点 Pn、Qn、Rn(n∈N*).设
,边AB上一点P1,这里P1异于A、B.由P1引边OB的垂线P1Q1,Q1是垂足,再由Q1引边OA的垂线Q1R1,R1是垂足.又由R1引边AB的垂线R1P2,P2是垂足.同样的操作连续进行,得到点 Pn、Qn、Rn(n∈N*).设 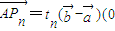 <tn<1),如图.
<tn<1),如图.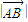 的值;
的值;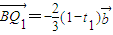 ,问该同学这个结论是否正确?并说明理由;
,问该同学这个结论是否正确?并说明理由;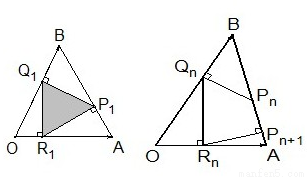
已知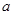 ,
,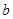 ,
,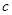 分别为
分别为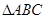 三个内角
三个内角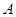 ,
,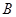 ,
,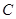 的对边,
的对边, .
.
(Ⅰ)求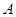 ;
;
(Ⅱ)若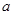 =2,
=2,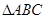 的面积为
的面积为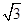 ,求
,求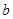 ,
,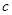 .
.
【命题意图】本题主要考查正余弦定理应用,是简单题.
【解析】(Ⅰ)由 及正弦定理得
及正弦定理得
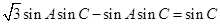
由于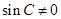 ,所以
,所以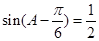 ,
,
又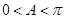 ,故
,故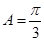 .
.
(Ⅱ) 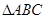 的面积
的面积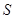 =
=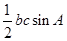 =
=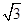 ,故
,故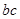 =4,
=4,
而 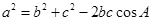 故
故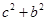 =8,解得
=8,解得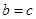 =2
=2
已知
 ,且
,且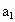 ,
,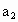 …,
…,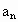 组成等差数列(n为正偶数),又
组成等差数列(n为正偶数),又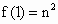 ,
, .
.
(1)
求数列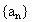 的通项;(2)试比较
的通项;(2)试比较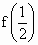 与3的大小,并说明理由.
与3的大小,并说明理由.
由所有既属于集合A又属于集合B的元素所成的集合,叫做A与B的________,记作A∩B,即A∩B={x|x∈A,且x∈B}.
可这样理解:交集A∩B是由两集合A与B的“公有”元素所组成的集合.用Venn图表示,如图.

易知:(1)若两集合A与B无公共关系,则A∩B=________;
(2)A∩B________A,A∩B________B;
(3)A∩A=________,A∩![]() =________,A∩B=B∩A;
=________,A∩B=B∩A;
(4)若A![]() B,则A∩B=________;若A∩B=A,则A________B;
B,则A∩B=________;若A∩B=A,则A________B;
(5)设U为全集,则A∩(![]() A)=________.
A)=________.
已知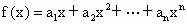 ,且
,且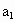 ,
,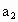 …,
…,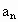 组成等差数列(n为正偶数),又
组成等差数列(n为正偶数),又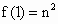 ,
,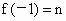 .
.
(1)求数列 的通项;(2)试比较
的通项;(2)试比较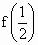 与3的大小,并说明理由.
与3的大小,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com