
题目列表(包括答案和解析)
A.过二面角的棱上某一特殊点,分别在两个半平面内引垂直于棱的射线,则这两条射线所成的角即为二面角的平面角
B.和二面角的棱垂直的平面与二面角的两个半平面的交线所成的角即为二面角的平面角
C.在二面角的一个面内引棱的垂线,该垂线与其在另一面内的射影所成的角是二面角的平面角
D.二面角的平面角可以是一个锐角、一个直角或一个钝角
A.过二面角的棱上某一特殊点,分别在两个半平面内引垂直于棱的射线,则这两条射线所成的角即为二面角的平面角
B.和二面角的棱垂直的平面与二面角的两个半平面的交线所成的角即为二面角的平面角
C.在二面角的一个面内引棱的垂线,该垂线与其在另一面内的射影所成的角是二面角的平面角
D.二面角的平面角可以是一个锐角、一个直角或一个钝角
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(Ⅰ)证明PC⊥AD;
(Ⅱ)求二面角A-PC-D的正弦值;
(Ⅲ)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.

【解析】解法一:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),D(2,0,0),C(0,1,0), 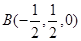 ,P(0,0,2).
,P(0,0,2).

(1)证明:易得 ,
, 于是
于是 ,所以
,所以
(2)  ,
, 设平面PCD的法向量
设平面PCD的法向量 ,
,
则 ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
.
所以二面角A-PC-D的正弦值为 .
.
(3)设点E的坐标为(0,0,h),其中 ,由此得
,由此得 .
.
由 ,故
,故
所以, ,解得
,解得 ,即
,即 .
.
解法二:(1)证明:由 ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以 .
.

(2)如图,作 于点H,连接DH.由
于点H,连接DH.由 ,
, ,可得
,可得 .
.
因此 ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
因此 所以二面角
所以二面角 的正弦值为
的正弦值为 .
.
(3)如图,因为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

在 中,由
中,由 ,
, ,
,
可得 .由余弦定理,
.由余弦定理, ,
,
所以 .
.
如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.

【解析】(Ⅰ)因为
又 是平面PAC内的两条相较直线,所以BD
是平面PAC内的两条相较直线,所以BD 平面PAC,
平面PAC,
而 平面PAC,所以
平面PAC,所以 .
.
(Ⅱ)设AC和BD相交于点O,连接PO,由(Ⅰ)知,BD 平面PAC,
平面PAC,
所以 是直线PD和平面PAC所成的角,从而
是直线PD和平面PAC所成的角,从而
 .
.
由BD 平面PAC,
平面PAC, 平面PAC,知
平面PAC,知 .在
.在 中,由
中,由
 ,得PD=2OD.因为四边形ABCD为等腰梯形,
,得PD=2OD.因为四边形ABCD为等腰梯形, ,所以
,所以 均为等腰直角三角形,从而梯形ABCD的高为
均为等腰直角三角形,从而梯形ABCD的高为 于是梯形ABCD面积
于是梯形ABCD面积
 在等腰三角形AOD中,
在等腰三角形AOD中,
所以
故四棱锥 的体积为
的体积为 .
.

【点评】本题考查空间直线垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明BD 平面PAC即可,第二问由(Ⅰ)知,BD
平面PAC即可,第二问由(Ⅰ)知,BD 平面PAC,所以
平面PAC,所以 是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由
是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由 算得体积
算得体积
如图,三棱锥 中,侧面
中,侧面 底面
底面 ,
,  ,且
,且 ,
, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面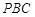 ;
;
(Ⅱ)若 为侧棱PB的中点,求直线AE与底面
为侧棱PB的中点,求直线AE与底面 所成角的正弦值.
所成角的正弦值.

【解析】第一问中,利用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以 第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证
第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,又EH//PO,所以EH平面
平面ABC,又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,

解
(Ⅰ) 证明:由用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以
………………………………………………6分
(Ⅱ)如图, 取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,
因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,
平面ABC,
又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,
且 ………………………………………10分
………………………………………10分
又PO=1/2AC= ,也所以有EH=1/2PO=
,也所以有EH=1/2PO= ,
,
由(Ⅰ)已证 平面PBC,所以
平面PBC,所以 ,即
,即 ,
,
故 ,
,
于是
所以直线AE与底面ABC 所成角的正弦值为

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com