
题目列表(包括答案和解析)
数列 的前n项和记为
的前n项和记为 ,前
,前 项和记为
项和记为
 ,对给定的常数
,对给定的常数 ,若
,若 是与
是与 无关的非零常数
无关的非零常数 ,则称该数列
,则称该数列 是“
是“ 类和科比数列”,
类和科比数列”,
(理科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列 的通项公式(5分);
的通项公式(5分);
(2)、证明(1)的数列 是一个 “
是一个 “ 类和科比数列”(4分);
类和科比数列”(4分);
(3)、设正数列 是一个等比数列,首项
是一个等比数列,首项 ,公比
,公比
 ,若数列
,若数列 是一个 “
是一个 “ 类和科比数列”,探究
类和科比数列”,探究 与
与 的关系(7分)
的关系(7分)
数列 的前n项和记为
的前n项和记为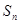 ,前
,前 项和记为
项和记为
 ,对给定的常数
,对给定的常数 ,若
,若 是与
是与 无关的非零常数
无关的非零常数 ,则称该数列
,则称该数列 是“
是“ 类和科比数列”,
类和科比数列”,
(理科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列 的通项公式(5分);
的通项公式(5分);
(2)、证明(1)的数列 是一个
“
是一个
“ 类和科比数列”(4分);
类和科比数列”(4分);
(3)、设正数列 是一个等比数列,首项
是一个等比数列,首项 ,公比
,公比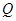
 ,若数列
,若数列 是一个
“
是一个
“ 类和科比数列”,探究
类和科比数列”,探究 与
与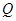 的关系(7分)
的关系(7分)
 的前n项和记为
的前n项和记为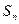 ,前
,前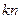 项和记为
项和记为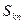
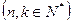 ,对给定的常数
,对给定的常数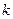 ,若
,若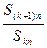 是与
是与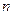 无关的非零常数
无关的非零常数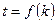 ,则称该数列
,则称该数列 是“
是“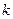 类和科比数列”,
类和科比数列”,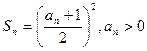 ,求数列
,求数列 的通项公式(5分);
的通项公式(5分);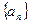 是一个 “
是一个 “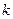 类和科比数列”(4分);
类和科比数列”(4分);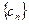 是一个等比数列,首项
是一个等比数列,首项 ,公比
,公比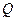
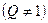 ,若数列
,若数列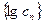 是一个 “
是一个 “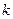 类和科比数列”,探究
类和科比数列”,探究 与
与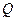 的关系(7分)
的关系(7分)若首项为 ,公比为q的等比数列
,公比为q的等比数列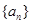 的前n项和总小于这个数列的各项和,则首项
的前n项和总小于这个数列的各项和,则首项 公比q的一组取值可以是
公比q的一组取值可以是 _________。
_________。
例10 为促进个人住房商品化的进程,我国1999年元月公布了个人住房公积金贷款利率和商业性贷款利率如下:
贷款期(年数)
公积金贷款月利率(‰)
商业性贷款月利率(‰)
……
11
12
13
14
15
……
……
4.365
4.455
4.545
4.635
4.725
……
……
5.025
5.025
5.025
5.025
5.025
……
汪先生家要购买一套商品房,计划贷款25万元,其中公积金贷款10万元,分十二年还清;商业贷款15万元,分十五年还清.每种贷款分别按月等额还款,问:
(1)汪先生家每月应还款多少元?
(2)在第十二年底汪先生家还清了公积金贷款,如果他想把余下的商业贷款也一次性还清;那么他家在这个月的还款总数是多少?
(参考数据:1.004455144=1.8966,1.005025144=2.0581,1.005025180=2.4651)
讲解 设月利率为r,每月还款数为a元,总贷款数为A元,还款期限为n月
第1月末欠款数 A(1+r)-a
第2月末欠款数 [A(1+r)-a](1+r)-a= A(1+r)2-a (1+r)-a
第3月末欠款数 [A(1+r)2-a (1+r)-a](1+r)-a
=A(1+r)3-a (1+r)2-a(1+r)-a
……
第n月末欠款数 
得:
对于12年期的10万元贷款,n=144,r=4.455‰
∴
对于15年期的15万元贷款,n=180,r=5.025‰
∴
由此可知,
(2)至12年末,

其中A=150000,a=1268.22,r=5.025‰ ∴X=41669.53
再加上当月的计划还款数2210.59元,当月共还款43880.12元.
需要提及的是,本题的计算如果不许用计算器,就要用到二项展开式进行估算,这在2002年全国高考第(12)题中得到考查.
例11 医学上为研究传染病传播中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠体内进行实验,经检测,病毒细胞的增长数与天数的关系记录如下表. 已知该种病毒细胞在小白鼠体内的个数超过108的时候小白鼠将死亡.但注射某种药物,将可杀死其体内该病毒细胞的98%.
(1)为了使小白鼠在实验过程中不死亡,第一次最迟应在何时注射该种药物?(精确到天)
(2)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命?(精确到天)
|