查看答案和解析>>

查看答案和解析>>

（1）用如图1所示的实验装置，验证牛顿第二定律．

①在平衡摩擦力时，先取下砂桶，将木板不带滑轮的一端垫高，让打点计时器接

交流电源

交流电源

（选填“交流电源”或“直流电源），然后

轻轻推动

轻轻推动

（选填“静止释放”或“轻轻推动”）小车，让小车拖着纸带运动．如果打出的纸带如图1右所示，则应

减小

减小

（选填“增大”或“减小”）木板的倾角，反复调节，直到纸带上打出的点迹

间隔均匀

间隔均匀

，平衡摩擦力才算完成．
②图2是某次实验中得到的一条纸带，则小车的加速度是

5.00

5.00

m/s²．（计算结果保留三位有效数字）
（2）①甲同学用多用电表测定一只电阻的阻值，操作如下：
多用电表电阻档有4个倍率：分别为×1K、×100、×10、×1．该同学选择×100倍率，用正确的操作步骤测量时，发现指针偏转角度太大（指针位置如图3中虚线所示）．为了较准确地进行测量，请你补充完整下列依次应该进行的主要操作步骤：
a．

重新选×10档测量

重新选×10档测量

；
b．两表笔短接，调节欧姆调零旋钮，使指针指在0Ω处；
c．重新测量并读数，若这时刻度盘上的指针位置如图中实线所示，测量结果是

120

120

Ω．
②乙同学用伏安法测量某金属丝的电阻（阻值5～10Ω），实验室提供了下列器材．
A．电压表（0～3V，内阻1kΩ）  B．电压表（0～15V，内阻5kΩ）
C．电流表（0～0.6A，内阻2Ω）      D．电流表（0～3A，内阻0.5Ω）
E．滑动变阻器（10Ω，0.2A）        F．滑动变阻器（50Ω，0.6A）
G．直流电源（6V，内阻不计）
另有开关一个、导线若干．
实验中有两种电路可供选择，如图4（甲）和（乙）所示．
本次实验中电路应选

乙

乙

（选填“甲”或“乙”），电压表应选

A

A

，电流表应选

C

C

，滑动变阻器应选

F

F

．（只填器材前的字母代号即可）．

查看答案和解析>>

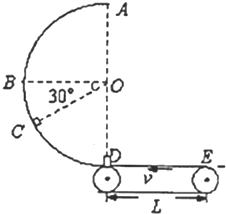如图所示，传送带以v为7

2

m/s速度向左匀速运行，DE段长L为4m，半径R为1.8m的光滑半圆弧槽在D点与水平传送带相切，半圆弧槽末端D点静止放置一质量m₂为0.4kg的小滑块Q，一质量m₁为0.2kg的小滑块P从C处无初速度滑下，到达最底端与小滑块发生弹性正碰，两滑块都可以视为质点，且与传送带间的动摩擦因数μ均为0.5，g取10m/s²，不计小滑块通过连接处的能量损失．求：
（1）小滑块P从C处无初速度滑下，到轨道底端D碰撞刚结束的瞬间速度
（2）小滑块Q第一次碰撞后向右运动的最大距离以及此过程产生的热量
（3）移走小滑块Q，将小滑块P无初速度放在传送带E端，要使小滑块能通过A点，传送带DE段至少为多长？

查看答案和解析>>

（1）如图1是利用重物自由下落验证机械能守恒定律的实验装置．质量 m=1.00kg 的重物自由下落，打点计时器在纸带上打出一系列点．如图所示为选取的一条符合实验要求的纸带，O 为第一个点，A、B、C 为从合适位置开始选取的三个连续点（其他点未画出）．已知打点计时器每隔 0.02s打一次点，当地的重力加速度 g=9.80m/s²
①某位同学做“验证机械能守恒定律”的实验，下列操作步骤中错误的是

 

A．把电磁打点计时器固定在铁架台上，用导线连接到低压交流电源
B．将连有重锤的纸带穿过限位孔，将纸带和重锤提升到一定高度
C．先释放纸带，再接通电源
D．更换纸带，重复实验，根据记录处理数据
②选取O点到B点来验证机械能守恒定律，重物重力势能减少量△E_P=

 

 J；动能增加量
△E_k=

 

 J．（结果取三位有效数字） 实验的结论是

 

．

（2）如图2某小灯泡上标有“6V 3W”字样，现要测量其正常发光时的实际电阻，实验室提供下列器材：
A、电压表量程（0～3V，内阻约2kΩ）
B、电压表量程（0～l5V，内阻约6kΩ）
C、电流表量程（0～0.6A，内阻约0.5Ω）
D、电流表量程量程2（0～3A，内阻约0.1Ω）
E、滑动变阻器 （20Ω，2A）
F、学生电源（直流10V）及开关、导线等
①实验中电压表量程应选择

 

（填“A”或“B”），
电流表量程应选择

 

（填“C”或“D”）；
②按照实验电路图在图甲中把实验的实物连线图补充完整；
③准确连接电路后，在闭合开关前滑动变阻器的滑片应该移到

 

端（填“最左”或“最右”）；
④闭合开关后，调节滑动变阻器使小灯泡达到其正常发光所需电压，此时电流表示数如图乙所示，则小灯泡的电阻的测量值为

 

．

查看答案和解析>>

题号

1

2

3

4

5

6

7

8

9

10

11

答案

C

B

A

D

D

A

D

C

B

B

C

题号

12

13

14

15

16

17

18

19

20

21

答案

D

B

C

AB

BC

AC

B

D

BD

C

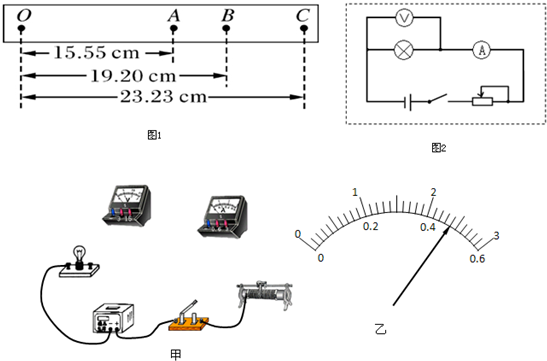
22．(Ⅰ)   甲     

（Ⅱ）

R₁=20   R₂=180    R₃=1.4 k

R₄=49.9 k   R₅=450 k

23．【解】当斜面体向右加速运动时，计算球离开斜面的临界加速度a₀，此时有：

Tsinθ-mg=0                              

Tcosθ=ma₀

由此解得：  a₀=gcotθ =m/s²

又    a=4m/s²> a₀

所以，小球离开斜面，设此时线与竖直方向成φ角，则：

Tsinφ-mg=0

Tcosφ=ma

解得：T=m=2.43N

24．解：如图所示，带电粒子从S点出发，在两筒之间的电场作用下加速，沿径向穿过狭缝a而进入磁场区，在洛伦兹力作用下做匀速圆周运动。粒子再回到S点的条件是能沿径向穿过狭缝d.只要穿过了d，粒子就会在电场力作用下先减速，再反向加速，经d重新进入磁场区，然后粒子以同样方式经过c、b，再回到S点。设粒子进入磁场区的速度大小为v，根据动能定理，有  

设粒子做匀速圆周运动的半径为R，由洛伦兹力公式和牛顿第二定律，有

由前面分析可知，要回到S点，粒子从a到d必经过圆周，所以半径R必定等于筒的外半径r，即R=r。由以上各式解得

25．解：用m表示A、B和C的质量。

（1）当物块A以初速度v₀向右运动时，它因受C给它的滑动摩擦力做匀减速直线运动，而它作用于C的摩擦力不足以使B、C产生相对滑动，即B、C以相同加速度做匀加速直线运动。物块A、B发生碰撞的临界情况是：物块A运动到物块B所在处时，A、B速度相等。

在临界状况下，因为B与木板C的速度始终相等，所以A、B即将碰撞时，A、B、C三者速度均相同，设为v₁。由动量守恒定律有

  mv₀=3mv₁    ①

在此过程中，设木板C 运动的路程为s₁，则物块A运动的路程为s₁+L，由功能原理得：

               ②

解①、②得：    

故A与B发生碰撞的条件是：

（2）当物块A的初速度时，A、B将发生碰撞，物块B与档板P发生碰撞的临界情况是：物块B运动到档板P所在处时，B、C的速度相等。同（1）中结论，在临界状况下，当B运动到档板P处时，A、B、C三者速度相等，设此速度为v₂，根据动量守恒定律得：

mv₀＝3mv₂        ③

   设A、B碰撞前瞬间，A、B、C速度分别为v_A、v_B和v_C，则v_A>v_B，v_B=v_C 。

   在A、B碰撞的极短时间内，A、B构成的系统的动量近似守恒，而木板C的速度保持不变，因为A、B间的碰撞是弹性的，即系统机械能守恒，又物块A、B质量相等，故易得：碰撞后A、B速度交换，设碰撞刚结束时A、B、C三者的速度分别为v_A?、v_B?、v_C?，则v_A?＝v_B，v_B?＝v_A，v_C?＝v_C，刚碰撞后A、B、C的运动与（1）类似，只是A、B的运动进行了交换，由此易分析：在整个运动过程中，先是A相对C运动的路程为L，接着是B相对C运动的路程为L，整个系统的动能转变为内能。类似（1）中方程得

       ④      

联立③、④解之，得：

故A与B相撞，B再与P相撞的条件是：

   （3）当物块A的初速度 时，B将与档板P相撞，撞后A、B、C的运动可由（2）中运动类比得到：B、P碰撞后瞬间，物块A、B速度相同，木板C速度最大，然后C以较大的加速度向右做减速运动，而物块A和B以相同的较小加速度向右做加速运动，加速过程将持续到或者A、B与C速度相同，三者以相同速度向右做匀速运动，或者木块A从木板C上掉了下来，因此物块B、A在木板C上不可能再发生碰撞。

(4)若A刚刚没从木板C上掉下来，即A到达C的左端时的速度变为与C相同，这时三者的速度皆相同，以v₃表示，由动量守恒有

                      3mv₃=mv₀                       ⑤

从A以初速度v₀在木板C的左端开始运动，经过B与P相碰，直到A刚没从木板C的左端掉下来，这一整个过程中，系统内部先是A相对C运动的路程为L，接着B相对C运动的路程也是L，B与P碰后直到A刚没从木板C上掉下来，A与B相对C运动的路程也皆为L，整个系统动能的改变应等于内部相互滑动摩擦力做功的代数和。

即：(3m)v₃²-mv₀² =-μmg?4L  ⑥

由⑤⑥两式得：

故A从C掉下的条件是：

（5）当物块A的初速度时，A将从木板C上掉下来。设A刚从木板C上掉下来时，A、B、C三者的速度分别为v_A″, v_B″, v_C″，有 v_A″＝ v _B″＜v_C″，这时⑤式应改写成

               mv₀=2m v_A″+mv_C″           ⑦

⑥式应改写成：   (2m)v_B″²+mv″_C²-mv₀=-μmg?4L     ⑧

当物块A掉下C后，物块B从木板C掉下的临界情况是：当C在左端赶上B时，B与C的速度相等，设此速度为v₄

则由动量守恒定律可得：   mv_B″+ mv_C″＝2mv₄             ⑨

再对B、C系统从A掉下C到B掉下C的过程用动能定律：

(2m)v₄² ―（mv″_B²+mv_C″²）= -μmgL     ⑩

联立⑦⑧⑨⑩，注意到v_A″＝ v _B″＜v_C″，可解得：

，，

故物块B从木板C上掉下的条件是：

26．（12分）（1）bd   （2分） （2）① 25%（2分）    23.1 kJ（2分）   ② ＞（2分） 

（3）阴（1分）  N₂ ＋ 6H⁺ + 6e^- ＝ 2NH₃（2分）

27．（18分）（1）acd（3分）   （2）HOCN（3分）  

（3）H―N=C=O（3分）    8HNCO + 6NO₂ = 7N₂ + 8CO₂ + 4H₂O（3分）

（4）NH+ OH^- NH₃↑+ H₂O（3分）    2.8%（3分）

（提示：c（HCl）= =0.08 mol?L^-1，

牛奶中蛋白质的百分含量）

28. （15分）（1）SiO₂＋2CSi＋2CO↑（3分）
（2）2Fe^2＋＋Cl₂＝2Fe^3＋＋2Cl^－（3分） 
H₂（g）＋Cl₂（g）＝2HCl（g）；ΔH＝－184.6 kJ?mol^－1（3分）
（3）N₂＋O₂2NO（3分）
（4）C＋4HNO₃CO₂↑＋4NO₂↑＋4H₂O（3分）

29. （15分）（1）HCHO  （各3分）
（2）①②⑤（3分）
（3）（3分）
（4）（3分）

30、（1）植物组织培养     (2分)

      取根尖分区制成装片，显微观察有丝分裂中期细胞内同源染色体数目．

若观察到同源染色体增倍，则属染色体组加倍所致；   

否则为基因突变所致  (6分)

（2）选用多株阔叶突变型石刀板雌、雄相交。

若杂交后代出现了野生型，则为显性突变所致；

若杂交后代仅出现突变型，则为隐性突变所致。(6分)

（3）选用多对野生型雌性植株与突变型雄性植株作为亲本杂交。.

若杂交后代野生型全为雄株，突变型全为雌株，则这对基因位于Ｘ染色体上；

若杂交后代，野生型和突变型雌、雄均有．则这对基因位于常染色体。(6分)

（4）已进化，生物的进化的实质在于种群基因频率的改变。(2分)

31．I．（1）甲装置中D中放入NaOH溶液（1分），装置乙作对照组（1分），

将装置甲、乙的玻璃钟罩遮光处理，放在温度等相同的环境中（3分）

（2）甲装置中D中放入NaHCO₃溶液（1分），装置乙作对照组（1分），

将装置甲、乙放在光照强度、温度等相同的环境中（3分）

（3）左（1分）、右（1分）

Ⅱ（1）4（2分）    12 （2分）     

（2）24（2分）