
题目列表(包括答案和解析)
 .
.| 1 | 2 |
已知a,b为两个正数,且a>b,设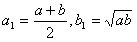 ,当n≥2,n∈N*时,
,当n≥2,n∈N*时,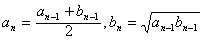 。
。
(1)求证:数列{an}是递减数列,数列{bn}是递增数列;
(2)求证:an+1-bn+1< ;
;
(3)是否存在常数C>0,使得对任意n∈N*,有|an-bn|>C,若存在,求出C的取值范围;若不存在,试说明理由。
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
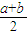 ,b1=
,b1=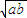 ,当n≥2,n∈N*时,an=
,当n≥2,n∈N*时,an=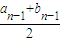 ,bn=
,bn=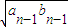 .
. (an-bn);
(an-bn);一.选择题
1―5 CBABA 6―10 CADDA
二.填空题
11. 12.(
12.( )
13.2
14.
)
13.2
14. 15.
15.
16.(1,4)
三.解答题

 17,解:①
17,解:①
 =2(1,0)
(2分)
=2(1,0)
(2分)
 ?
? ,
(4分)
,
(4分)
|