题目列表(包括答案和解析)
已知曲线C：
的横坐标分别为1和
，且a1=5，数列{xn}满足xn+1 = tf (xn – 1) + 1（t > 0且
）．设区间
，当
时，曲线C上存在点
使得xn的值与直线AAn的斜率之半相等．
证明：
是等比数列；
当
对一切
恒成立时，求t的取值范围；
记数列{an}的前n项和为Sn，当
时，试比较Sn与n + 7的大小，并证明你的结论．
(13分) 已知曲线C：
的横坐标分别为1和
，且a1=5，数列{xn}满足xn+1 = tf (xn – 1) + 1（t > 0且
）．设区间
，当
时，曲线C上存在点
使得xn的值与直线AAn的斜率之半相等．
(1) 证明：
是等比数列；
(2) 当
对一切
恒成立时，求t的取值范围；
(3) 记数列{an}的前n项和为Sn，当
时，试比较Sn与n + 7的大小，并证明你的结论．
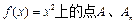的横坐标分别为1和
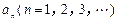，且a1=5，数列{xn}满足xn+1 = tf (xn – 1) + 1（t > 0且
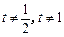）．设区间
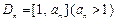，当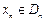
时，曲线C上存在点
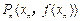使得xn的值与直线AAn的斜率之半相等．
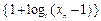是等比数列；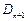
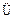
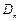对一切
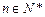恒成立时，求t的取值范围；
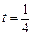时，试比较Sn与n + 7的大小，并证明你的结论．已知曲线C：f(x)＝x2上的点A、An的横坐标分别为1和an(n＝1，2，3，…)，且a1＝5，数列{xn}满足xn+1＝tf(xn－1)＋1(t＞0且t≠
，t≠1)．设区间Dn＝[1，an](an＞1)，当xn∈Dn时，曲线C上存在点Pn(xn，f(xn))使得xn的值与直线AAn的斜率之半相等．
(1)证明：{1＋logt(xn－1)}是等比数列；
(2)当Dn+1
Dn对一切n∈N*恒成立时，求t的取值范围；
(3)记数列{an}的前n项和为Sn，当t＝
时，试比较Sn与n＋7的大小，并证明你的结论．
已知曲线C：f(x)＝x2上的点A、An的横坐标分别为1和an(n＝1，2，3，…)，且a1＝5，数列{xn}满足xn+1＝tf(xn－1)＋1(t＞0且t≠
，t≠1)．设区间Dn＝[1，an](an＞1)，当xn∈Dn时，曲线C上存在点Pn(xn，f(xn))使得xn的值与直线AAn的斜率之半相等．
(1)证明：{1＋logt(xn－1)}是等比数列；
(2)当Dn+1
Dn对一切n∈N*恒成立时，求t的取值范围；
(3)记数列{an}的前n项和为Sn，当t＝
时，试比较Sn与n＋7的大小，并证明你的结论．
一．选择题
1―5 CBABA 6―10 CADDA
二．填空题
11．
12．（
）
13．2
14．
15．
16．（1，4）
三．解答题
17，解：①
=2(1,0)
（2分）
?
，
（4分）
|
cos
=
， 
， 
即B=
（7分）
（9分）
， 
（11分）
的取值范围是(
,1
（13分）
(
) （1分）
,求得两焦点
,
（3分）
,又
为一条渐近线
, 解得:
（5分）
（6分）
，则
（7分）
?
（9分）
， 
（10分）
（11分）
（13分）
单减区间为[
] （6分）
（8分）
，
, (
)，
，
（10分）
，
（11分）
在（0，1]上单调递减 
（12分）
（13分）
（2分）
}是首项为1，公差为C的等差数列
即
（4分）
即
………………※
（6分）
（8分）
（9分）
（
）
（11分）
（12分）
的切线斜率为K，则切线方程：
（2分）
即
（3分）
又
（4分）
（5分）
， 
（6分）
可得：
（8分）
（9分）
（11分）
，取 “=”，此时
（12分）
， 
故
即证
（
）
（1分）
即：
（3分）
（
（6分）
（8分）
（10分）
（11分）
（12分）