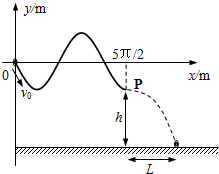18．如图所示.一金属杆弯成如图所示形状的固定导轨.左侧导轨处于水平面内.右侧导轨处在倾角θ＝30°的斜面上.前后导轨的间距处处都为l．质量为m.电阻为R的金属棒ab水平放置在倾斜的导轨上．整个装置处——青夏教育精英家教网—

18．如图所示.一金属杆弯成如图所示形状的固定导轨.左侧导轨处于水平面内.右侧导轨处在倾角θ＝30°的斜面上.前后导轨的间距处处都为l．质量为m.电阻为R的金属棒ab水平放置在倾斜的导轨上．整个装置处在方向垂直于斜面的匀强磁场中.磁感应强度为B．给棒一定的初速度.可使棒恰好沿斜面匀速下滑.然后再进入水平轨道滑行．不计整个导轨的电阻和摩擦.重力加速度为g．求: (1)金属棒沿斜面匀速下滑的速度v0．【查看更多】

如图所示，将一根质量为M=0.06kg的均匀导线杆弯成矩形闭合导线框abcd，其ab=cd=L₁=0.1m，bc=ad=L₂=0.2m．它的ad边由aO、dO′两轴承支撑沿水平放置，导线框位于竖直平面内，bc段中点固定一质量为m=0.02kg的小金属球，整个装置处在一方向竖直向上的匀强磁场中．当导线框中通以大小恒为1A的恒定电流I时，整个装置以OO′为轴从静止开始逆时针转动．
（1）在图中画出导线框bc段中的电流方向；
（2）若导线框运动过程中与竖直方向的最大偏角θ为37°，则匀强磁场的磁感应强度B₁为多大？（已知sin37°=0.6，cos37°=0.8）
（3）若已知磁感应强度B₂=1T，则导线框在运动过程中，速度达到最大时，与竖直方向的偏角α为多大．

查看答案和解析>>

如图所示，在竖直向下，场强为E的匀强电场中，长为l的绝缘轻杆可绕固定轴O在竖直面内无摩擦转动，两个小球A、B固定于杆的两端，A、B的质量分别为m₁和m₂（m₁＜m₂），A带负电，电量为q₁，B带正电，电量为q₂．杆从静止开始由水平位置转到竖直位置，求：
（1）在此过程中电场力所做的功为多少？
（2）在竖直位置处两球的总动能为多少？
若将轻杆弯折成如图所示的“Γ”形，两边互相垂直、长度均为

1

2

，两端各固定一个金属小球A、B，在竖直向下，场强为E的匀强电场中，可绕过O点的水平轴在竖直平面内无摩擦转动．已知A球质量m₁=m，电量为+q，B球质量m₂=7m/2，B球也带负电，电量为-q．现将“Γ”形杆从OB位于水平位置由静止释放，求：
（3）OB杆能转过的最大角度为127°，则该电场强度的大小为多少？
（4）当两球的速度达到最大时，OB杆转过的角度为多大？

查看答案和解析>>

如图所示，在理想边界MN的上方有方向向右的匀强电场E，下方有垂直纸面向外的磁感应强度大小为B=0.20T的匀强磁场，电场和磁场的范围足够大．一根光滑的绝缘塑料细杆abcd弯成图示形状，其中ab段是竖直的，bcd正好构成半径为R₁=0.20m的半圆，bd位于边界MN上，将一个质量为m=0.10kg、电量为q=0.50C的带正电金属环套在塑料杆ab上，从距离b点高R处由静止开始释放后，g=10m/s²．求：
（1）金属环经过最低点c处时对塑料杆的作用力；
（2）如果金属环从d点进入电场后，正好垂直打在塑料杆ab段上，求电场强度E的大小．

查看答案和解析>>

如图所示，将一个光滑金属杆弯成y=-2sinx（0≤x≤

5π

2

）（单位：m）的形状，一个小环从x=0处以沿着杆的初速v₀出发，最终从x=

5π

2

处的P点水平抛出，下落高度h=1.8m后掉落在地面上．试求
（1）v₀满足什么条件时小环才能从P点水平抛出？
（2）小环从P点水平抛出的射程L和v₀的函数关系式是怎样的？

查看答案和解析>>

如图所示，用两根金属丝弯成一光滑半圆形轨道，竖直固定在地面上，其圆心为O、半径为0.3m．轨道正上方离地0.4m处固定一水平长直光滑杆，杆与轨道在同一竖直平面内，杆上P点处固定一定滑轮，P点位于O点正上方．A、B是质量均为2kg的小环，A套在杆上，B套在轨道上，一条不可伸长的细绳绕过定滑轮连接两环．两环均可看作质点，且不计滑轮大小与质量．现在A环上施加一个大小为55N的水平向右恒力F，使B环从地面由静止沿轨道上升．（g取10m/s²），求：
（1）在B环上升到最高点D的过程中恒力F做功为多少？
（2）当被拉到最高点D时，B环的速度大小为多少？
（3）当B、P间细绳恰与圆形轨道相切时，B环的速度大小为多少？
（4）若恒力F作用足够长的时间，请描述B环经过D点之后的运动情况．

查看答案和解析>>

13．（10分）（1）ADEF．（2）不变；放．（每空2分）

14．（10分）（1）ACE．（2）0.4 ；y轴正方向．（每空2分）

15．（11分）

（1）右端（1分），v_A ＝0.72 m/s（2分），v_B＝0.97 m/s（2分）．

（2）G，B（每空2分）

（3）（2分）