设数列{a_n}满足a₁＝2，a_n+1＝2a_n+2，用数学归纳法证明a_n＝4·2^n-1-2的第二步中，设n＝k时结论成立，即a_k＝4·2^k-1-2，那么当n＝k+1时，a_k+1为

1. A.
   4·2^k-2
2. B.
   4·2^k+1-2
3. C.
   4·2^k-1-2
4. D.
   4·2^k+2-2

设集合M＝{－1,0,1}，N＝{x|x²≤x}，则M∩N＝ (   )

A．{0}               B．{0,1}             C．{－1,1}           D．{－1,0,1}

在数列{a_n}中，a₁＝1，＝＋．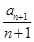

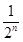(1)设b_n＝，求数列{b_n}的通项公式；

(2)求数列{a_n}的前n项和S_n．

设全集U＝A∪B＝{x∈N^*|lgx＜1}，若A∩(∁_UB)＝{m|m＝2n＋1，n＝0,1,2,3,4}，则集合B＝________.

设集合M＝{－1,0,1}，N＝{x|x²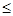x}，则M∩N＝(　　)

A．{0}               B．{0,1}             C．{－1,1}           D．{－1,0,1}