
题目列表(包括答案和解析)
解::因为![]() ,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=
,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=![]() 与y=-
与y=-![]() 在(0,+
在(0,+![]() )上都是增函数,因此
)上都是增函数,因此![]() 在(0,+
在(0,+![]() )上是增函数,所以零点个数只有一个方法2:把函数
)上是增函数,所以零点个数只有一个方法2:把函数![]() 的零点个数个数问题转化为判断方程
的零点个数个数问题转化为判断方程![]() 解的个数问题,近而转化成判断
解的个数问题,近而转化成判断![]() 与
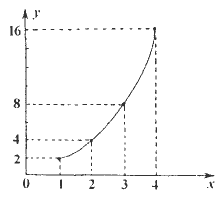
与![]() 交点个数问题,在坐标系中画出图形
交点个数问题,在坐标系中画出图形
由图看出显然一个交点,因此函数![]() 的零点个数只有一个
的零点个数只有一个
袋中有50个大小相同的号牌,其中标着0号的有5个,标着n号的有n个(n=1,2,…9),现从袋中任取一球,求所取号码的分布列,以及取得号码为偶数的概率.
(14分) 已知二次函数![]() 为偶函数,函数
为偶函数,函数![]() 的图象与直线y=x相切.
的图象与直线y=x相切.
(1)求![]() 的解析式
的解析式
(2)若函数![]() 上是单调减函数,那么:
上是单调减函数,那么:
①求k的取值范围;
②是否存在区间[m,n](m<n为了了解已有沙漠面积1000万公顷的某地区沙漠面积的变化情况,环保监测部门进入了连续4年的观察,并将每年年底的观察结果记录如表甲.根据这些数据还可绘制曲线图乙.由此预测到该地区沙漠的面积将继续扩大.
表甲

图乙
(1)如果不采取任何措施,那么到第m年底,该地区沙漠面积变为多少公倾?
(2)如果第5年底后,采取引水和植树造林等措施,使沙漠化扩大趋势得以减缓.第6年开始的每一年年底观察得该地区沙漠面积比上一年增加数y(公顷)分别为:a6,a7,a8,…,an,而a6,a7,a8,…,an还构成首项a6=32,公差d=-8的递减等差数列.当沙漠化扩大趋势停止后(即an=0),每年改造18万公顷沙漠,那么第n年底,该地区沙漠的面积能减少到980万公顷?
(本小题满分16分)知函数f(x)=ax3+bx2+cx+d(a、b、c、d![]() R),且函数f(x)的图象关于原点对称,其图象x=3处的切线方程为8x-y-18=0.
R),且函数f(x)的图象关于原点对称,其图象x=3处的切线方程为8x-y-18=0.
(1)求f(x)的解析式;
(2)是否存在区间![]() ,使得函数f(x)的定义域和值域均为
,使得函数f(x)的定义域和值域均为![]() ?若存在,求出这样的一个区间
?若存在,求出这样的一个区间![]() ;若不存在,则说明理由;
;若不存在,则说明理由;
(3)若数列{an}满足:a1≥1,an+1≥![]() ,试比较+++…+与1的大小关系,并说明理由.
,试比较+++…+与1的大小关系,并说明理由.
(本题满分12分)
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
|
|
感染 |
未感染 |
总计 |
|
没服用 |
20 |
30 |
50 |
|
服用 |
x |
y |
50 |
|
总计 |
M |
N |
100 |
设从没服用疫苗的动物中任取两只,感染数为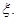 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为 工作人员曾计算过
工作人员曾计算过
(1)求出列联表中数据 的值;
的值;
(2)写出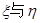 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
(3)能够以97.5%的把握认为这种甲型H1N1疫苗有效么?并说明理由。
参考公式:
参考数据:
|
|
0.05 |
0.025 |
0.010 |
|
|
3.841 |
5.024 |
6.635 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com