
题目列表(包括答案和解析)
对于不等式![]() ≤n+1(n∈N+),某学生证明过程如下:
≤n+1(n∈N+),某学生证明过程如下:
(1)当n=1时,![]() ≤1+1,不等式成立.
≤1+1,不等式成立.
(2)假设当n=k(k∈N+)时,不等式成立,即![]() ≤k+1.那么,当n=k+1时,
≤k+1.那么,当n=k+1时,![]() =
=![]() <
<![]() =
=![]() =(k+1)+1.
=(k+1)+1.
这表明,当n=k+1时,不等式成立.
对于上述证法,下列判断正确的是________.
①过程全部正确;
②n=1验证不正确;
③归纳假设不正确;
④从n=k到n=k+1的推理不正确.
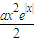 对于n∈R恒成立.
对于n∈R恒成立.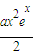 成立?如果存在,求出符合条件的一个x;否则说明理由.
成立?如果存在,求出符合条件的一个x;否则说明理由.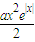 对于n∈R恒成立.
对于n∈R恒成立.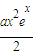 成立?如果存在,求出符合条件的一个x;否则说明理由.
成立?如果存在,求出符合条件的一个x;否则说明理由. ,
, 中,
中, ,且
,且 是函数
是函数 的一个极值点。
的一个极值点。 的通项公式;
的通项公式; 图像上的点
图像上的点 的切线始终与
的切线始终与 平行(O 为原点),求证:当
平行(O 为原点),求证:当 且t≠1时,不等式
且t≠1时,不等式 对任意n∈N*都成立。
对任意n∈N*都成立。
|
| 5cmn |
| cmcn |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0 | ||||||
| 2 | 0 | ||||||
| 3 | 0 | ||||||
| 4 | 0 | ||||||
| 5 | 0 | ||||||
| 6 | 0 | ||||||
| 7 | 0 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com