
题目列表(包括答案和解析)
设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1; 以M2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.考察下列论断:
当n=1时,| A1B1 |=2;
当n=2时,| A2B2 |= ;
;
当n=3时,| A3B3 |= ;当n=4时,| A4B4
|=
;当n=4时,| A4B4
|= ;
;
……
由以上论断推测一个一般的结论:对于n∈N*,| AnBn |= ▲ .
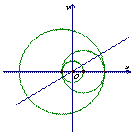 设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1;以M2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.考察下列论断:
设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1;以M2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.考察下列论断:
当n=1时,![]() ;Ks当n=2时,
;Ks当n=2时,![]() ;当n=3时,
;当n=3时,![]() ;
;
当n=4时, ![]() ;当n=5时,
;当n=5时, ![]() ;……,
;……,
则推测一个一般的结论:对于n∈N*,![]() .
.
设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1;以M2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作
⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……
当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.
考察下列论断:
当n=1时,| A1B1 |=2;Ks*5u
当n=2时,| A2B2 |=![]() ;
;
当n=3时,| A3B3 |=![]() ;
;
当n=4时,| A4B4 |=![]() ;
;
……
由以上论断推测一个一般的结论:
对于n∈N*,| AnBn |= .
设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1;以M![]() 2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作
2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作
⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……
当n∈N*时,过原点作倾斜角为30°的直线![]() 与⊙Mn交于An,Bn.考察下列论断:
与⊙Mn交于An,Bn.考察下列论断:
当n=1时,| A1B1 |=2;当n=2时,| A2B2 |=![]() ;当n=3时,| A3B3 |=
;当n=3时,| A3B3 |=![]() ;
;
当n=4时,| A4B4 |=![]() ;……
;……
由以上论断推测一个一般的结论:对于n∈N*,| AnBn |= ![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com