
题目列表(包括答案和解析)
函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
(1)求实数a,b,并确定函数 的解析式;
的解析式;
(2)判断 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
【解析】本试题主要考查了函数的解析式和奇偶性和单调性的综合运用。第一问中,利用函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
解得 ,
,
(2)中,利用单调性的定义,作差变形判定可得单调递增函数。
(3)中,由2知,单调减区间为 ,并由此得到当,x=-1时,
,并由此得到当,x=-1时, ,当x=1时,
,当x=1时,
解:(1) 是奇函数,
是奇函数, 。
。
即 ,
, ,
, ………………2分
………………2分
 ,又
,又 ,
, ,
, ,
,
(2)任取 ,且
,且 ,
,
 ,………………6分
,………………6分
 ,
,
 ,
, ,
, ,
, ,
,
 在(-1,1)上是增函数。…………………………………………8分
在(-1,1)上是增函数。…………………………………………8分
(3)单调减区间为 …………………………………………10分
…………………………………………10分
当,x=-1时, ,当x=1时,
,当x=1时, 。
。
设函数 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
已知等比数列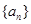 中,
中,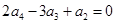 ,且
,且 ,公比
,公比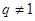 ,(1)求
,(1)求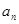 ;(2)设
;(2)设 ,求数列
,求数列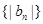 的前
的前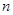 项和
项和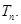
【解析】第一问,因为由题设可知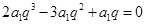
又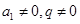 故
故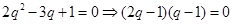
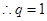 或
或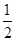 ,又由题设
,又由题设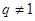
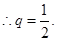 从而
从而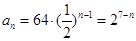
第二问中,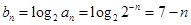
当 时,
时,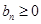 ,
, 时
时
故 时,
时,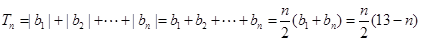
 时,
时,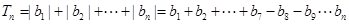
分别讨论得到结论。
由题设可知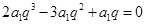
又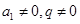 故
故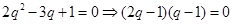
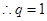 或
或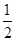 ,又由题设
,又由题设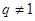
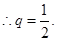
从而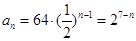 ……………………4分
……………………4分
(2)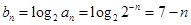
当 时,
时,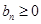 ,
, 时
时 ……………………6分
……………………6分
故 时,
时,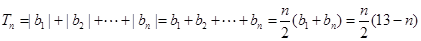 ……8分
……8分
 时,
时,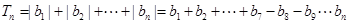
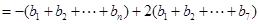
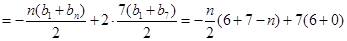
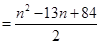 ……………………10分
……………………10分
综上可得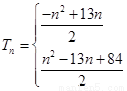

已知幂函数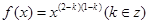 满足
满足 。
。
(1)求实数k的值,并写出相应的函数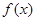 的解析式;
的解析式;
(2)对于(1)中的函数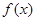 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数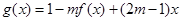 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
【解析】本试题主要考查了函数的解析式的求解和函数的最值的运用。第一问中利用,幂函数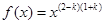 满足
满足 ,得到
,得到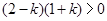
因为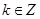 ,所以k=0,或k=1,故解析式为
,所以k=0,或k=1,故解析式为
(2)由(1)知,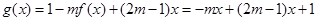 ,
, ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: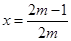 ,结合二次函数的对称轴,和开口求解最大值为5.,得到
,结合二次函数的对称轴,和开口求解最大值为5.,得到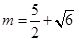
(1)对于幂函数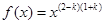 满足
满足 ,
,
因此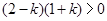 ,解得
,解得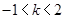 ,………………3分
,………………3分
因为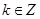 ,所以k=0,或k=1,当k=0时,
,所以k=0,或k=1,当k=0时, ,
,
当k=1时, ,综上所述,k的值为0或1,
,综上所述,k的值为0或1, 。………………6分
。………………6分
(2)函数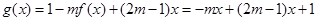 ,………………7分
,………………7分
由此要求 ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: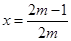 ,
,
当 时,
时,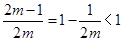 ,因为在区间
,因为在区间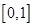 上的最大值为5,
上的最大值为5,
所以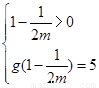 ,或
,或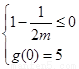 …………………………………………10分
…………………………………………10分
解得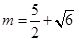 满足题意
满足题意
P(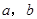 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“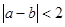 ”,其中
”,其中 为实常数.
为实常数.
(1)若 均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若 均为从区间[0,5)任取的一个数,求事件A发生的概率.
均为从区间[0,5)任取的一个数,求事件A发生的概率.
【解析】本试题考查了几何概型和古典概型结合的一道综合概率计算试题。首先明确区域中的所有基本事件数或者区域表示的面积,然后分别结合概率公式求解得到。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com